前回は「進化距離」の意味から、最も単純な進化距離の計算手法である「P-distance(P距離)」についてご説明させて頂きました。
今回はもう少し複雑な進化距離の指標であるポアソン距離(Poisson Correction distance/Poisson distance)についてご紹介します。
まず結果から書くと、ポアソン距離による進化距離の公式は下記のようになります。
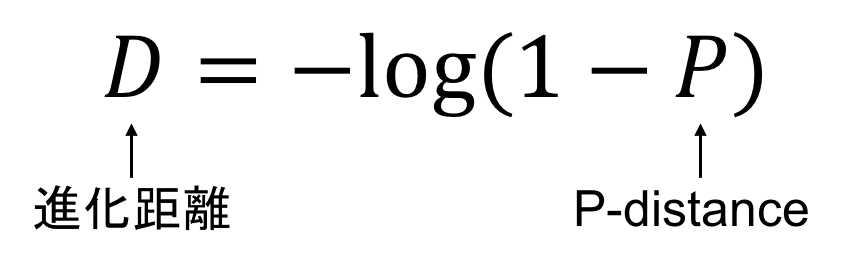
なぜか、logなんて出てきます。
本ポストでは、P-distanceの問題点を提示した上で、そのポアソン距離の導出方法について説明します。
P-distanceの復習
さて、「進化距離」とは、2つの生物のDNAの違いの大きさを数値化したものでした。
その計算の方法は山ほどある中で、もっとも単純と言える方法がP-distanceです。
計算方法は単純で、「2つの配列を並べた時、不一致箇所の割合はどれだけの割合か?」を調べるだけです。
例えば下図のような2配列ならば、7箇所中3箇所が異なっているので、割合としては3/7=約0.429となり、
「生物Aと生物BのP-distanceによる進化距離は0.429」というように表現されます。

ちなみに、配列の長さが違う場合の対処については、前回記事をご確認頂ければと思います。
P-distanceの問題点
さて、上記のようにシンプルな計算で求められるP-distanceですが、一長一短があります。
P-distanceは、「秋田犬と柴犬」のように近い生物同士を比べる時には大変有効なのですが、
「ヒトとペンギン」のように遠いと思われる生物同士を比べると不都合が生じます。
なぜでしょうか?それはDNAの進化のプロセスを考える必要があります。
先程の図の一番左は、生物Aが「C」と生物Bが「T」という事で異なっています。
これは、「もともとの共通祖先ではCだったが、共通祖先から生物Bへの進化の過程で、CがTに変異した」
もしくは、「もともとの共通祖先ではTだったが、共通祖先から生物Aへの進化の過程で、TがCに変異した」
のいずれかと考えられ、「変異が1回起こっている」と見なしている訳です。
しかし、本当にそれだけでしょうか。
例えば、「もともとの共通祖先ではGだったが、共通祖先から生物Aへの進化の過程で、GがCに変異し、共通祖先から生物Bへの進化の過程で、GがTに変異した」
という場合もあれば、
「もともとの共通祖先ではCだったが、共通祖先から生物Bへの進化の過程で、CがGになり、GがTに変異した」という場合だってあり得る訳です。
こうなると、「変異が2回起こっている」ということになります。
つまり、生物Aが「C」と生物Bが「T」という情報だけでは、変異が1回なのか2回なのか、はたまたそれ以上なのかは分からない訳です。
P-distanceは、「変異回数が最小の場合」の計算をしているに過ぎないのです。
近い生物同士ならばDNAの変異の回数は少ないと思われるので大きな問題はないのですが、
遠い生物同士だとDNAの変異の回数は多いと思われるので、「変異回数が最小の場合」で見積もるP-distanceを使うのは少々向かない、と考えられます。
これが、本項の最初の方で述べた「P-distanceは、近い生物同士を比べる時には大変有効だが、遠い生物同士を比べると不都合が生じる」という話につながる訳です。
複数回数の変異を考慮した進化距離「ポアソン距離」
P-distanceでは、DNAの同じ場所が複数回変わるパターン(これを「多重置換」と言います)には対応できない事が分かりました。
では、多重置換を考慮するにはどうすればよいのでしょうか。
その問題を解決する進化距離こそが、今回ご紹介する「ポアソン距離」になります。
P-distanceの問題点やポアソン距離が重要な背景についての説明はここまでで、ここからは本記事の冒頭に書いたポアソン距離の公式の導出方法についての話になります。
ここからはほとんど数式ばかりなので、結果だけ知りたいという方は読み飛ばして頂いて問題ありません(笑)
ちなみに、ポアソン距離の導出方法を知りたいという方に限らず、微分方程式に興味のある方もお読み頂けると良いかなと思います。
ポアソン距離の導出方法
まず、「1年で1つのDNAが変異する確率」というものを導入し、これをλ(ラムダ)と置きます。
これは「DNA全体のうち、1年で変異する場所の割合がλ」と見なせます。
また、祖先が同じだった時から今までの時間をtと置きます。
すると、「共通祖先が生物Aに進化した現在までに、DNAが異なっている場所の存在割合」はλtとなります。
(DNAの変異はそうそう発生するものではないので、λtは1を超えないという前提に基づきます。)
同様に、「共通祖先が生物Bに進化した現在までに、DNAが異なっている場所の存在割合」もλtとなります。
ということは、「生物Aと生物Bの間で、DNAが変異している場所の割合」は、λt+λt=2λtとなります。
「生物Aと生物Bの間で、DNAが変異している場所の存在割合」というのは、そのまま生物Aと生物Bの進化距離であると考えられます。
よって、進化距離をDと置くと、以下の関係性が言えます。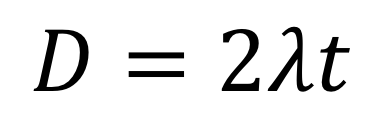
t年目とt+1年目の関係
次は、進化途中のt年目とt+1年目の関係性を考えてみます。
共通祖先から分岐後t年目におけるP-distanceをP(t)と置きます。
つまりP(t)は「分岐後t年目で、異なっているペアの存在割合」です。
逆に、1-P(t)は「分岐後t年目で、同じペアの存在割合」となります。
さて、ではP(t+1)をP(t)を用いて表してみましょう。
まず、P(t)に当たる「既に異なっているペア」は、「同じペア」に戻ることはありません(※)ので、そのまま引き継ぎます。
(※同じペアに戻ることを仮定する進化距離もありますが、ポアソン距離では考慮しません。)
次に、1-P(t)に当たる「同じペア」については、その一部が「違うペア」に変わってしまいます。
・・・さて、「1年で1つのDNAが変異する確率」がλでした。
「同じペア」が「違うペア」に変わってしまうパターンとしては、「生物Aが変異する場合」「生物Bが変異する場合」の2つに分けられますので、1-P(t)のうち、1年間で2λが「違うペア」に変わってしまうと計算できます。
(生物Aと生物Bがどちらも変異する場合もありますが、極めて稀なことなので0と見なします。)
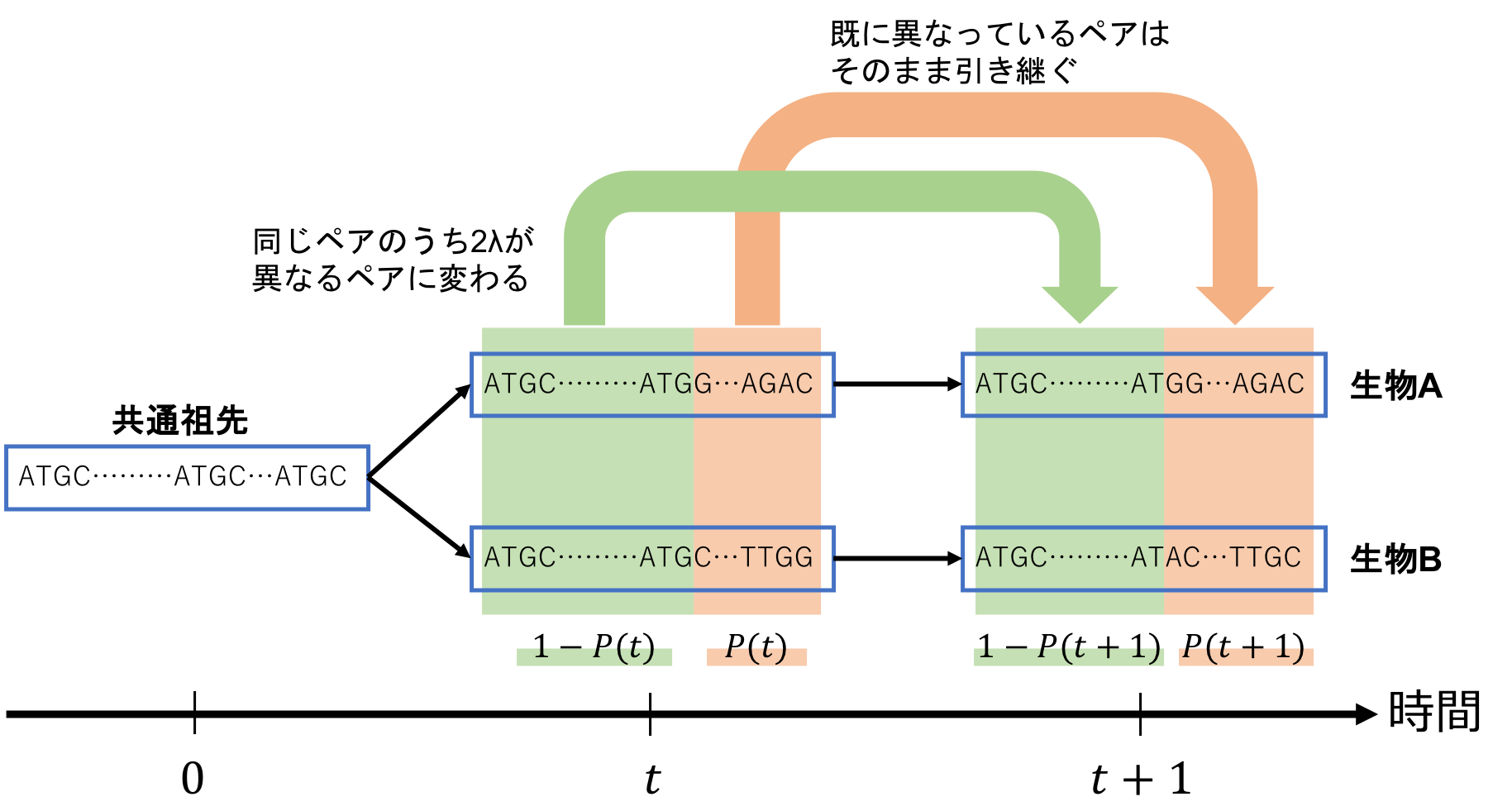
そして、これらを式で表すと、以下の関係性が導出できます。
方程式を解く
さて、先程1つの式を立てました。この方程式を解いてみましょう。
まず、P(t)を左辺に移行します。
するとP(t+1)-P(t)というのは、「1年あたりのPの変化量」になります。
ここで「1年」というのは、進化の長い長い歴史からすると非常に微小な値になります。
そして、1年を微小量と見なせるのならば、左辺はP(t)を微分したものと同値と言えます。
よって、上の式は以下のように書き換えられます。
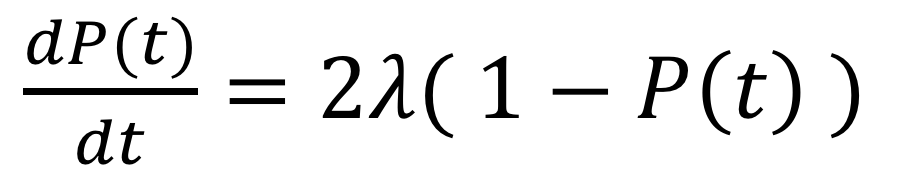
これは紛れもない「微分方程式」ですね。この式を解けば、P(t)が計算できそうです。
ちなみに、計算の途中でP(0)の値が必要となりますが、
P(0)は「生物が分岐してから0年経過時の、異なっているペアの存在割合」です。
分岐してから0年、ということは全く分岐していないのと同じですので、P(0)=0だと分かります。
では、計算してみます。
これで微分方程式が計算できました。
P(t)を進化距離の式に代入
さて、進化距離Dは2λtと書けるのでした。よく見ると上記の微分方程式の左辺と一致しています。
また、P(t)は、分岐してからt年目(現在)の「異なるペア」の存在割合なので、まさにP-distanceの定義と一緒です。
ということで、冒頭に示した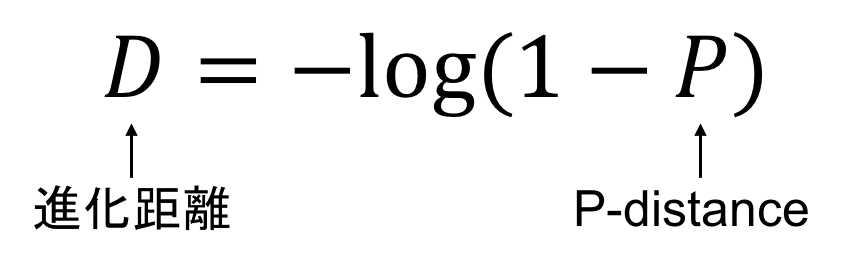
が導出できました。
こうして、P-distanceでは考慮できなかった「多重置換」を考慮した、ポアソン距離による進化距離の導出が完了しました。
AからCになってまたAに戻る「復帰置換」や、DNAの変異だけでなく、増えたり無くなったりする「挿入欠失」など、さらに複雑な状況を加味した進化距離もたくさんありますが、それらの多くはこのポアソン距離の考え方が基本となっています。