２クラス混同行列とその評価指標〜再現率、適合率、F値、など〜

AIの精度評価をする時や、データ集計の際にによく用いられる混同行列(Confusion matrix)についてです。
また、そこから計算される色々な性能指標についても整理します。
（よく間違われますが、「混合行列」ではないのでご注意下さい。）

今回は、「ある画像がネコか、それともネコでは無いのか？」など、分類が2パターンだけの「2クラス分類」についてとなります。
それ以上の「多クラス分類」については別記事に整理しています。

多クラス混同行列とその評価指標〜マクロ平均、マイクロ平均〜

混同行列とは

混同行列とは、あるデータを分類したときに、その正解・不正解の数を整理しておく表のことです。
ただそれだけの事なのですが、実は「正解」「不正解」といっても、それぞれ2パターンの意味があります。

例えば、動物の画像を見て、それがネコかどうか判断させるAIを作ったとします。
「正解」には「ネコの画像を正しくネコと判断できた」と「ネコ以外の画像を正しくネコではないと判断できた」の2パターン。
同様に、「不正解」には、「ネコの画像をネコではないと判断した」と「ネコ以外の画像をネコと判断した」の2パターン。
正解・不正解を振り分けるだけでも実は4パターンあるわけです。

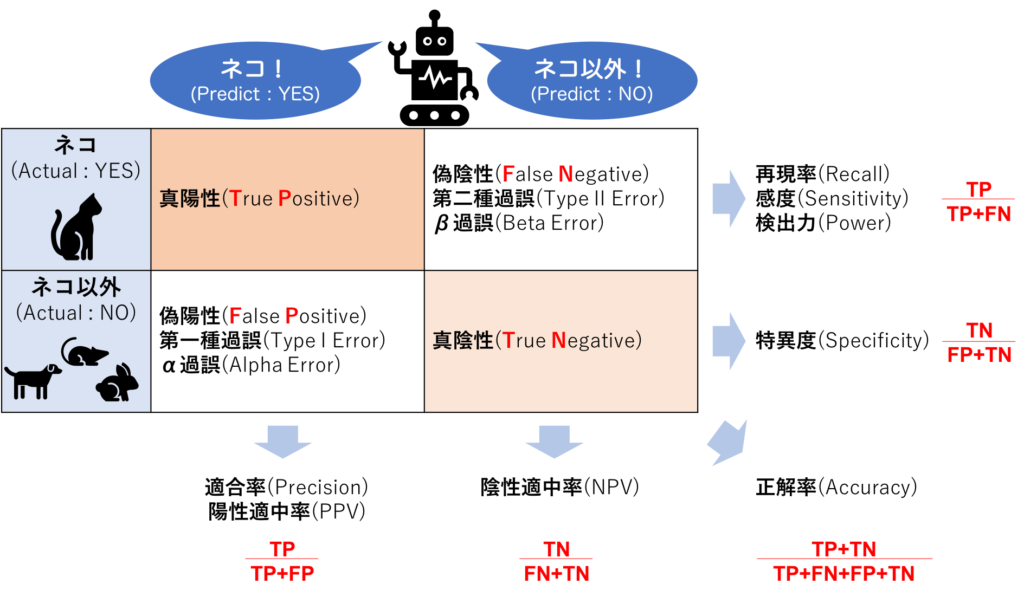
図にすると以下のようになります。（数値は一例）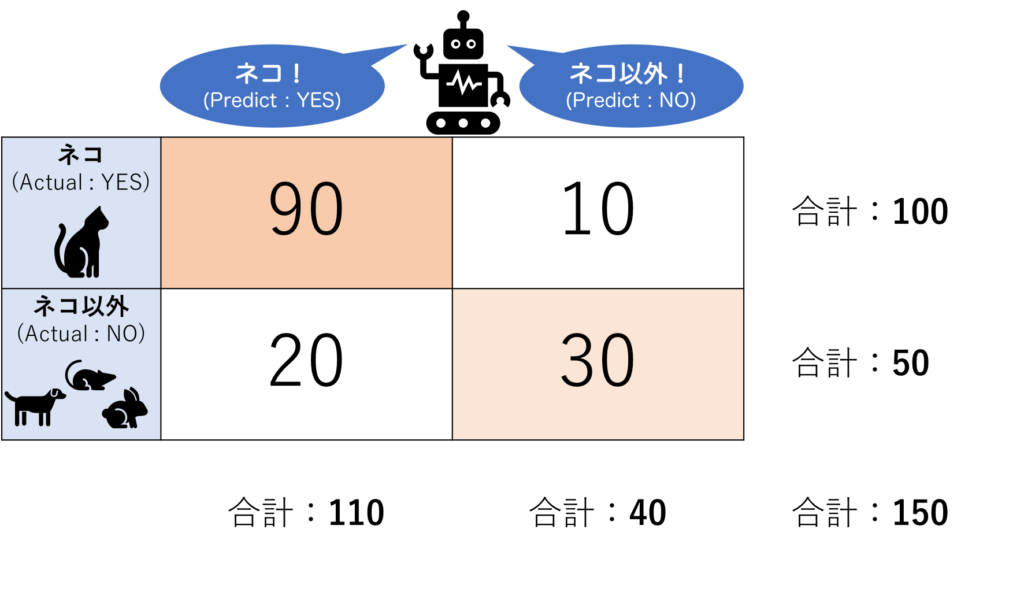

そして、この「4パターン」にはそれぞれ名称がついています。

真陽性(True Positive)

判別したいものを正しく判別できた数を「真陽性」、英語でTrue Positiveと呼びます。
上の例で言えば、「ネコの画像(Positive)を正しく(True)ネコと判別した」数で、左上の「90」がそれに当たります。

真陰性(True Negative)

判別対象外のものを正しく判別できなかった数を「真陰性」、英語でTrue Negativeと呼びます。
上の例で言えば、「ネコ以外の画像(Negative)を正しく(True)ネコ以外と判別した」数で、右下の「30」がそれに当たります。

偽陽性(False Positive)

判別対象外のものを誤って判別してしまった数を「偽陽性」、英語でFalse Positiveと呼びます。
上の例で言えば、「ネコ以外の画像(Negative)を間違えて(False)ネコと判別した」数で、左下の「20」がそれに当たります。
こちらは別名「第一種過誤」や「α過誤」とも呼ばれます。

偽陰性(False Negative)

判別したいものを誤って判別できなかった数を「偽陰性」、英語でFalse Negativeと呼びます。
上の例で言えば、「ネコの画像(Positive)を間違えて(False)ネコ以外と判別した」数で、右上の「10」がそれに当たります。
こちらは別名「第二種過誤」や「β過誤」とも呼ばれます。

混同行列における精度指標

さて、表に整理したことによって正解・不正解の状況（分類の精度の良さ）が分かりやすくなりました。
しかし、数をカウントしただけなので、一体このAIの精度が何%なのかはまだ分かりません。

混同行列から精度を算出する方法は何通りもあり、どの計算方法が最善なのかは時と場合によって異なります。
どう使い分けるかは一度置いておき、まずはどういった算出方法があるのかを見ていきます。

正解率(Accuracy)

最も単純な指標です。
全データのうち、正解したデータ数の割合です。
上の例で言うと、全150データのうち、90+30=120枚正解していますので、
正解率は120/150=80.0%と計算されます。

再現率(Recall)

判別したいデータの数のうち、実際に判別できた割合です。
つまり、ネコのデータの中で、どれだけ正解できたか？ということになります。
よって、上の例では90/100=90.0%と計算されます。

再現率は、別名「感度(Sensitivity)」や「検出力(Power)」とも呼ばれます。

特異度(Specificity)

判別したくないデータの数のうち、実際に判別されなかった割合です。
つまり、ネコ以外のデータの中で、どれだけ正解できたか？ということになります。
上の例では30/50=60.0%と計算されます。

適合率(Precision)

“判別対象のデータ”を判別した数のうち、それが正解している割合です。
つまり「ネコ！」と判別された画像のうち、それが実際にネコの画像である割合です。
上の例では90/110=約81.8%と計算されます。

別名、「陽性適中率(Positive Predictive Value)」とも呼ばれます。

陰性適中率(Negative Predictive Value)

“判別対象外のデータ”を判別した数のうち、それが正解している割合です。
つまり「ネコ以外！」と判別された画像のうち、それが実際にネコ以外の画像である割合です。
上の例では、30/40=75.0%と計算されます。

混同行列とその性能指標のまとめ

以上を図にまとめます。
同じ場所に書かれた用語は、すべて同じ意味です。
文献などによっては行列の縦横が逆のものもありますので、ご注意ください。

組み合わせによる指標

さて、混同行列から直接読み取れる性能指標は上で示したもので全てですが、上の指標同士を組み合わせて計算する指標も幾つか存在するのでご紹介します。

F値(F-measure)

F値とは、再現率と適合率の調和平均です。

補足

「調和平均」というのは、「逆数の平均の逆数」で定義されます。
例えば4と6の調和平均は、1/4と1/6の平均が5/24なので、それをひっくり返した24/5(=4.8)となります。
「確率」や「割合」といった値の平均値を取りたい場合にはこの「調和平均」が良く用いられます。

一般的に再現率と適合率はトレードオフの関係にあります。
トレードオフとは、「再現率が上がると適合率が下がる」「適合率が上がると再現率が下がる」という関係です。

再現率と適合率を一方に偏らせずに均等に評価したい、という場合にF値が使われます。
上の例では、再現率が90.0%、適合率が81.8%なので、その調和平均の約85.7%が「F値」となります。

性能指標の使い分け方

これまで書いてきたように、性能指標にも色々あることがわかりました。
しかし大切なのは、「どんな時、どんな指標を使えばよいのか？」という事です。
どの指標にも一長一短があり、様々な観点から、そのタスクに応じた最善の評価指標を選ぶ必要があります。
そして、いくらAIが発達しても、評価指標を選ぶのは人間です。ここを疎かにしてはいけません。

参考として、「正解率」「再現率」「適合率」「F値」のメリット・デメリットを整理しておきます。

	メリット	デメリット
正解率	最もシンプルで分かりやすい	クラスごとの評価データ数が著しく異なると不適切
再現率	取りこぼしを発見できる	過検知を発見できない
適合率	過検知を発見できる	取りこぼしを発見できない
F値	取りこぼし、過検知をどちらも均等に判断できる	数値の解釈が難しくなる