以下は2004年〜2018年の日本にある公衆電話台数の推移を表したグラフです。
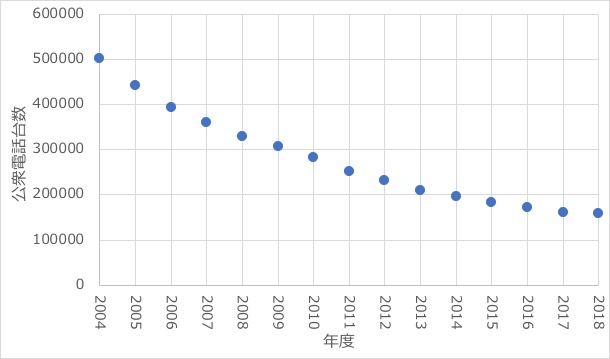
(※参考:総務省HP)
さて、この情報を元に、5年後(2023年)の、日本にある公衆電話の台数を予測してみましょう。
そのために、このグラフの傾向を表す「近似線」を引くことになるわけですが、直線を使うべきでしょうか、曲線を使うべきでしょうか。
試しに、直線と曲線の2パターンで近似線を引いてみます。
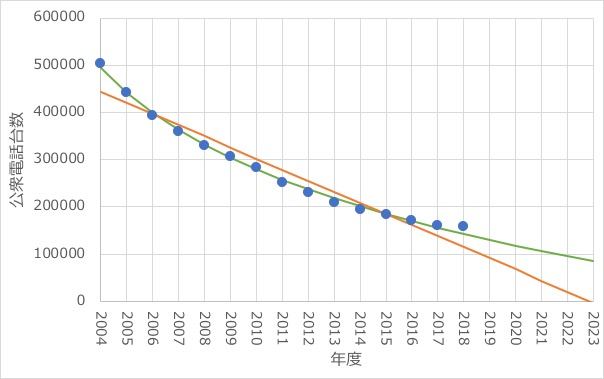
直線(オレンジ)で引くと、5年後の公衆電話台数がマイナスになってしまっています。
曲線(緑)で引くと、5年後の公衆電話台数は約8〜9万台と計算されます。
いくら公衆電話が減ってもマイナスになることはあり得ないので、直線で近似するのは流石におかしいと分かります。
このように、近似線を引いたり回帰分析を行ったりする時、データによっては直線では無く曲線を用いるべき時が良くあります。
いわゆる「曲線あてはめ」「カーブフィッティング」などとも呼ばれます。
しかし、ひとえに曲線といっても様々な種類があります。一体、どういう時にどういう曲線を選べばよいのでしょうか?
本記事では、Excelの「近似曲線」オプションにある「指数近似」「線形近似」「対数近似」「多項式近似」「累乗近似」に限り、適切な曲線を選ぶためのひとつの方針を示します。
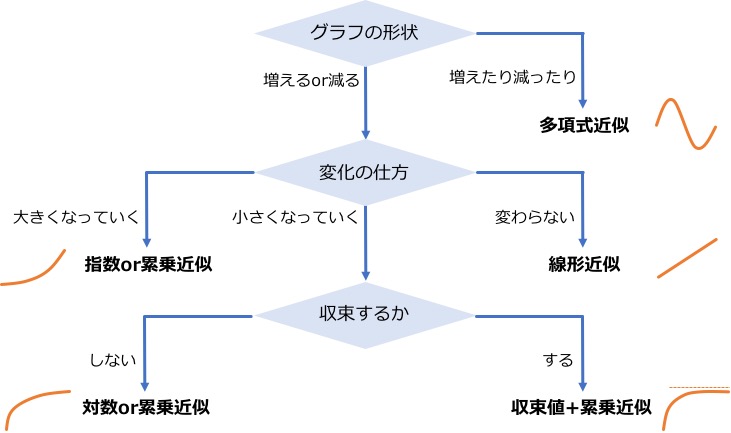
適切な曲線の選び方
グラフの形状はどうなっている?
グラフが「増えるor減る一方」なのか、「増えたり減ったりする」のかを考えます。
増減の大きさが微量であればこの限りではありませんが、下図のように明らかに「増えたり減ったりする」のならば、Excelでは多項式近似しかありません。
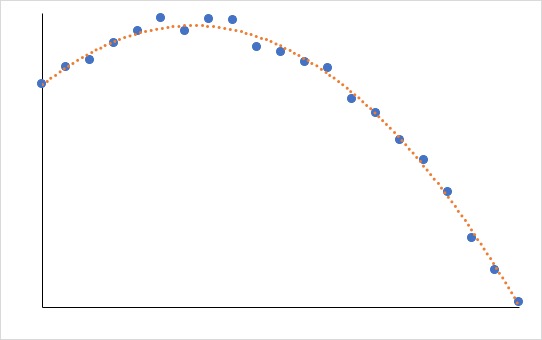
「増えて、減る」or「減って、増える」なら2次関数。「増えて、減って、増える」or「減って、増えて、減る」なら3次関数・・・というように、多項式の次数は波の数に合わせましょう。
とはいえ、あくまで完璧では無い「近似」の線ですから、5次、6次関数のような高次元の方程式で当てはめても解釈が難しくなりますし、そもそも過学習(後述)の可能性が高いです。
個人的には、実用を考えるとせいぜい2次関数、稀に3次関数くらいが限度かなと考えます。
・・・さて、そうではなく、「増える一方」「減る一方」の傾向の場合は、次のフローに移ります。
変化量は大きくなっていく?小さくなっていく?
xが1つ増えるごとにyが変わる量を「変化量」と言います。
「変化量がほぼ一定」であれば、「線形近似」一択です。
「変化量が一定」というのは、以下のように完全なる直線関係のことです。
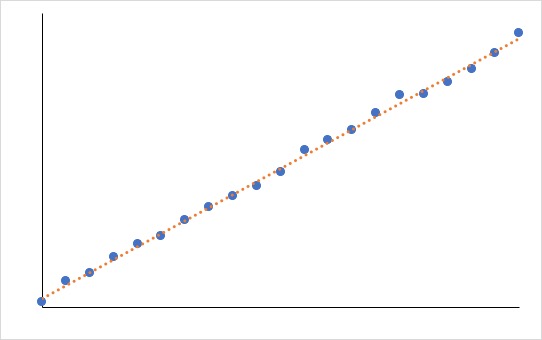
そうではなく、x=1,2,3,4,5の時にy=1,2,4,7,11,16…となるような、徐々に変化量が大きくなっていく場合があります。
その時、グラフは以下のようになります。
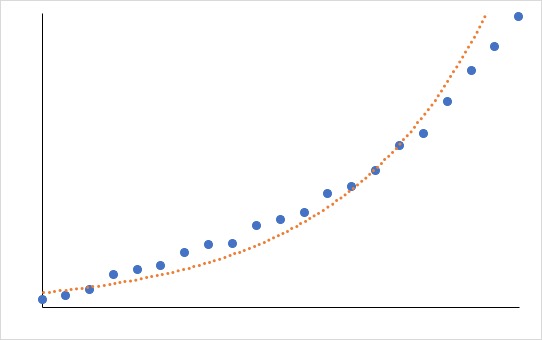
このように、「変化量が大きくなっていく」のであれば、「指数近似」か「累乗近似」を選びましょう。
指数近似が良いか、累乗近似が良いかについての明確な線引きは難しいのですが、後ほどその選択のためのアイデアを示します。
では、今度は「変化量が小さくなっていく」場合ですが、これはまた1つ深いフローに移ります。
値は収束するか、しないか?
値が収束しない場合とは、以下のようにゆっくりながらも、際限なく値が増え続けるor減り続けるという状態。
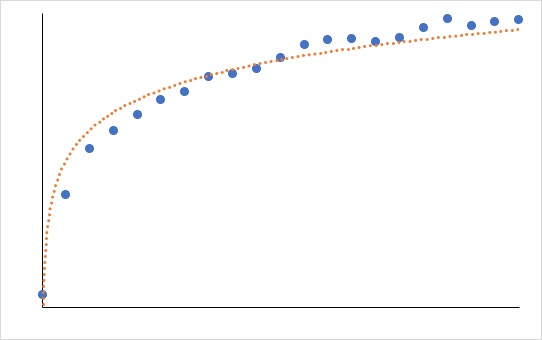
このように、「値が収束しない場合」であれば、「対数近似」か「累乗近似」を選びましょう。
先程と同様に、対数近似が良いか、累乗近似が良いかについては後ほど。
もう1つ、値が収束する場合とは、以下のように「いくら増えても絶対に100は超えない」といった、上限or下限が定まっている状態。
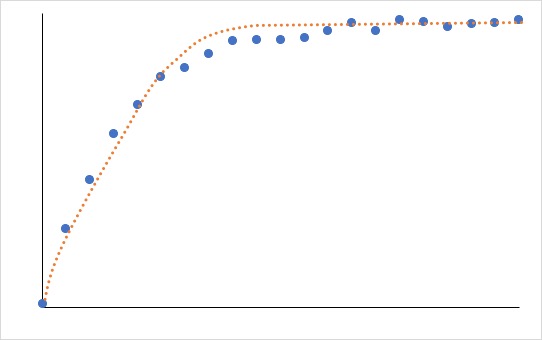
このように「値が収束する場合」であれば、「収束値」+「累乗近似」という方法で近似しましょう。
このオプションはExcelの機能には無いのですが、自分で「収束値-x」の列を作り、その列に対して「累乗近似」を使えばOKです。
収束値が0の場合は、そのまま累乗近似を行えば問題ありません。
収束する値が不明な場合は、Excelで近似曲線を書くのは少々難しいかなと思います。
このように、グラフの形状は近いものの「収束するか」or「収束しないか」、この2つは明確に区別しなければいけません。
例えば、縦軸が確率である場合、何をどう頑張っても100%以上や0%以下にはなりませんので、収束しない曲線を使うのはおかしいと考えられます。
指数近似/対数近似を選ぶか、累乗近似を選ぶか?
さて、変化量が大きくなっていく場合は、「指数近似」or「累乗近似」。
変化量が小さくなっていき収束しない場合は「対数近似」or「累乗近似」、と書きました。
しかし「or」と言われても、一体どっちを選ぶべきなのでしょうか。
ここは一概には言えない所がありますが、適切な曲線を選択するための考え方を幾つか示します。
解析したいデータはどんなデータなのか
データによっては、「これは指数関数になるはずだ」「これは累乗関数になるはずだ」というものがあります。
以下のページに実例が載っていますので、ご参照ください。
(※参考:MicrosoftOfficeサポートページ「データに最適な近似曲線を選択する」)
上記ページの例のように、扱っているデータが「この曲線になるはずだ」という確信があるのなら、たとえ他の曲線の方が当てはまりが良かったとしてもそちらを選択した方が良いでしょう。
logやeを用いても問題ないか?
データ分析結果を、分析業務に関与していない方へ説明する事があります。
こういった時、あまりlogとかeとかを出したくないなんていう時があります。
logとかeとかが出てくるだけでその資料自体に抵抗を持たれてしまう場合がありますので・・・。
累乗くらいならば良いかと思いますが、logやeを資料に使っても問題なさそうかきちんと考えておきましょう。
数式は美しいか?
これには賛否両論あるかと思われますが、私は数式の見た目・分かりやすさをわりと重要視します。
例えば、累乗近似したときに、「xのa乗」という部分が出てきます。
aが0.5くらいだったり0.33くらいだったりしたら、それはxの二乗根・三乗根と書き換えられるので、数式が非常にさっぱりした見た目にも美しい近似式が出来上がります。
少々昔の情報になりますが、「システム開発における最適な工期は投入人月の立方根の2.4倍」という報告がありました。
おそらく、うまくいった開発の人月(x)と工期(y)のデータを沢山集めて、累乗近似を行ったらy = 2.4x0.33くらいになったのでしょう。
「立方根の2.4倍」と端的に関係性を言い表せるのは良いですね。
R2値は幾つか?
特に上記3つを考えても、どっちとも選べない場合は、R2値を見ると良いと思います。
Excelの近似曲線オプションで簡単に表示できます。
R2値が1に近いほど、「今あるデータ」への当てはまりが良い、と考えることができます。
一般的に、「回帰分析の精度を測る際にはまずR2値を見ましょう」といった説明が成されます。
勿論、それは正しいのですが、今回は敢えて優先順位を一番下に持ってきました。
理由としては、当てはまりが良いからと言って優れた近似だとは限らないことと、本来、曲線近似においてR2値は計算しないことがあります。
1つ目の問題は、いわゆる「過学習」や「オーバーフィッティング」と呼ばれるものです。
これは、「未知のデータ」を予測するために近似しているのに、「今あるデータ」の事しか考えられていない状態です。
一般的に、「今あるデータ」が絶対に正しいと過信しすぎると、「未知のデータ」の予測精度が下がります。
データというのは大抵、間違えがあったり、少々誤差があるものですので、基本的に「今あるデータ」はゆるーく信じてあげることが大事です。
あまりにも近似線が当てはまり過ぎの場合は、その結果を疑うことも必要です。
2つ目の問題ですが、Excelの近似曲線オプションではいずれもR2値を計算してくれます。
しかし、一般的に曲線近似においてR2値は算出するものではありません。
これはExcelが間違えているという訳ではなく、Excelでは一般的でない計算でR2値の算出を行っているからです。
もちろんこの値を当てに出来ないわけでは無いのですが、一般的に言われるR2値とは少し違うもの、とお考えください。
詳細については、以下のページなどをご参照ください。
(※参考:エクセル近似曲線の罠)
まとめ
さて、今回、細かい数学的な面は排除してお話させて頂きました。
もちろん数学的な理解も大事ですが、データ分析において大切なのは、あくまでも「分析しようとしているデータは、一体どんな特徴を持ったデータなのか」という事を一生懸命に考えることです。
最後に、最適な近似曲線選択のためのフローを1枚にまとめておきます。
こちらを参考に、より良い曲線近似・回帰分析を行って頂ければ幸いです。