「t検定」を正しく理解しよう

例えば、ある会社の全社員に「あなたにとってこの会社は100点中何点ですか？」というアンケートを取ったとします。
その結果、全社員の平均値が昨年60点だったのが、今年は80点に上がりました。
この結果を見ると、多くの方は社員満足度が向上したと考えると思います。

しかし、昨年60点で、今年が62点だとしたらどうでしょう。
今度は「本当に上がったの？」と思われる方が多くなるのではないでしょうか。

つまり後者は、点数が上がってはいるけど「誤差の範囲内」ではないか？と思えるわけです。
しかし、具体的にどこまでが「誤差の範囲」なのでしょう？
そんな時は、本日紹介するt検定の出番です。

t検定とは

t検定とは別名「平均値の検定」とも呼ばれており、「データ1の平均値」と「データ2の平均値」が等しいと見なせるか、見なせないかを統計学的に判断するための手法で、「仮説検定」のひとつです。
（仮説検定にはt検定以外も様々な手法があります。）

この2つのデータでt検定を行うと、「p値」という0〜1の値が出力されます。

このp値が2つのデータ群に差があるかどうかを判断するキモになり、p値が「決めた値(よく用いられるのは0.05)」より小さければ「2つのデータには差がある」と判断することができます。

t検定を行う前に確認すべきポイント

t検定はいかなるデータに対しても用いて良いわけではありません。
t検定を行う際に注意しないといけない事、決めておかないといけない事を列挙します。

データは正規分布に従うか？

まず、t検定を行う前提条件として、「データが正規分布に従っていること」が必要です。

簡単に調べるのであれば、Excelなどでデータのヒストグラムを書いてみて、正規分布のような形状になっているか見てみるのも良いでしょう。
精密に行うには、Excelでは難しいですがQ-Qプロットや正規性の検定を用いる事となります。

【Python】正規分布に従っているかを調べる手法3種

そしてデータの分布を調べた結果、「流石にこれは正規分布じゃないな」という場合もあります。
こういった際にはt検定は不適切なので、分布を仮定しない検定手法を適用することを考えます。
（以下の記事もご参照ください。）

仮説検定の手法一覧と、それらの使い分け方

「増えたor減った」のを調べたいのか、「差がある」のを調べたいのか？

いわゆる「片側検定」「両側検定」の使い分けです。

「今年は昨年よりも増えたor減ったのか?」を見たいのならば「片側検定」を使います。
どちらが高い低いは関係なく、「昨年と今年で差が出ているのか？」を見たいのならば、「両側検定」を使います。

片側検定なのか両側検定なのかは人間が決めなければいけませんので、検証したい内容に合致する方を選びましょう。

比較する2回の調査で、対象が同じか？

冒頭で示した例で言えば、「アンケートを取った社員が昨年と今年で同じか、違うか」という事になります。

同じである方がより正確な評価が出来るのですが、一般的には退職者や新入社員などが居るので調査対象は変わるでしょう。
どちらの場合でもt検定の適用は可能ですが、計算方法が少々異なるので注意が必要です。
（Excelでの方法については後述します。）

比較する2回の調査で、分散は同程度か？

今年のデータと昨年のデータの分散の大きさが違うかどうかで、適用する手法が変わります。
分散が異なる時は「ウェルチのt検定(Welch’s t-test)」という手法を用いるのですが、分散が等しくてもウェルチのt検定を用いて問題ない・・・という意見もあります。

なので、ExcelのVAR.P関数などで、「昨年」と「今年」のそれぞれの分散を調べてそれらが同じくらいかどうか確認し、
2つの分散値が全然違うか、悩むレベルであれば「分散が異なる」と考えて良いかと思います。

有意水準は幾つにするか？

2データにどれだけ差があるとしても、それが「偶然じゃない！」と100%言い切ることはできません。
どんなに異なっていても、0.0001%くらいはそれが偶然で発生する可能性はあります。

では、一体、どれ以上の差があれば「差が出ている！」と言ってしまえるのでしょうか。
そのためには、「有意水準」を設定する必要があります。

「有意水準」とは、「p値がこの値を下回ったら、2つのデータには差がある」と判定する基準値です。

慣例的には0.05はよく用いられます。
つまりp値が0.05を下回っていれば、「有意差がある」と見なします。
より精密に行いたいならばこの水準を0.01とする場合もあります。

・・・しかし、ここが大事なのですが、結果を見てから水準を動かしてはいけません。
それはずるいです。
一般的に有意水準は検定を行う前に決めておき、あとから動かすことはしません。

Excelの関数を用いたt検定

さて、ここまで決めればt検定が実行できます。
関数を使う方法と、「データ分析」機能を使う方法がありますが、まずは関数を使う方法から。

Excelの関数でt検定を行うには、T.TEST関数を使います。
上記で決定した内容を、下記の通り引数に反映します。

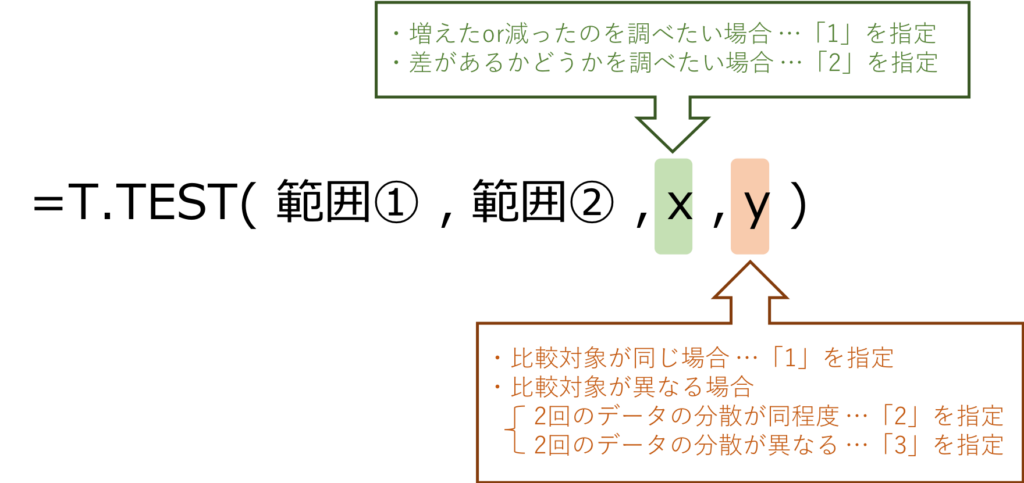
全6パターンで計算してみた例が以下になります。
（今回はパターン全てで行っていますが、実際は適切な手法を1つ選んでから適用します。）

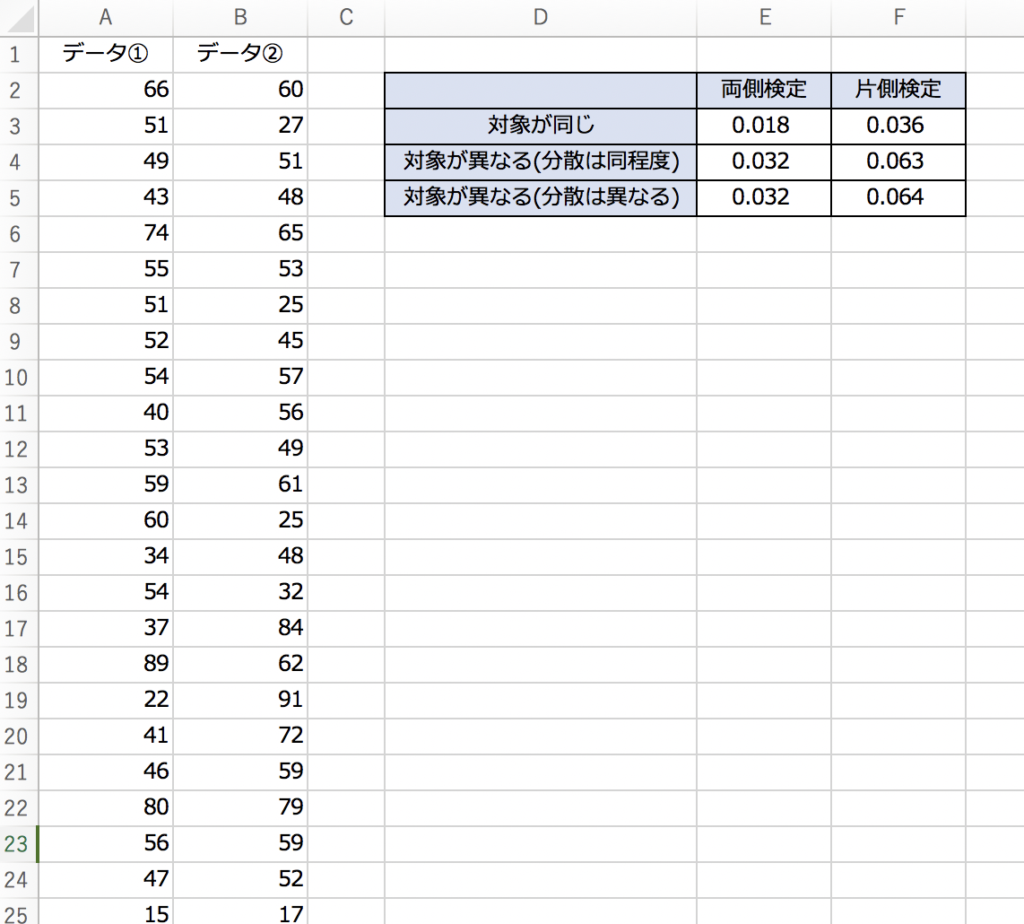
見て分かるとおり、t検定の前提条件によって結果は変わります。なので、検定を実行する前に前提条件をきちんと設定しておかねばなりません。
そして、「p値を幾つにするか」という問題に限らず、結果が出てから都合の良いものを選んではいけません。

Excelの「データ分析」機能を用いたt検定

「データ分析」機能を使ってもt検定ができます。
関数を使うよりもこちらの方が早く、かつ細かい結果が得られます。

「データ」タブから「データ分析」を起動すると、t検定に関わる項目が3つ出てきます。

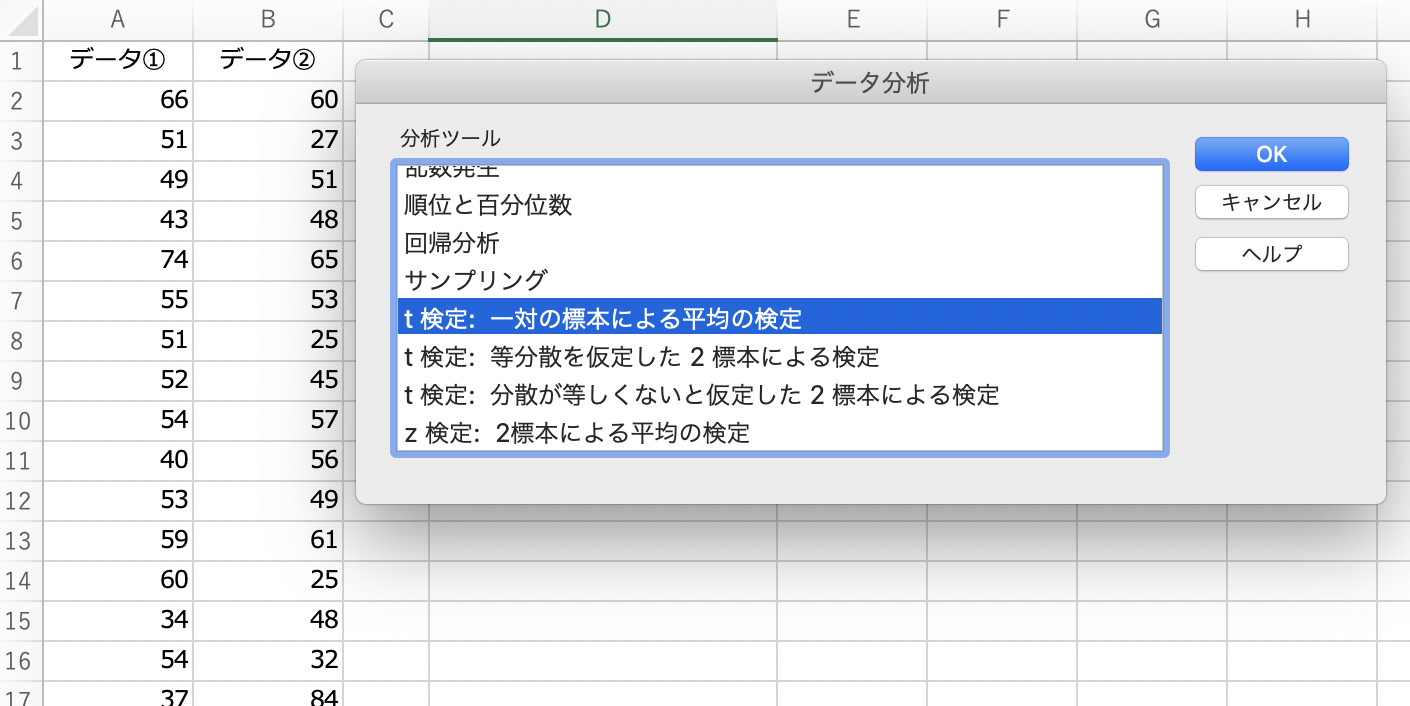
まさに、先述した3パターンですね。
では、今回は「t検定:一対の標本による平均の検定」を実行してみます。

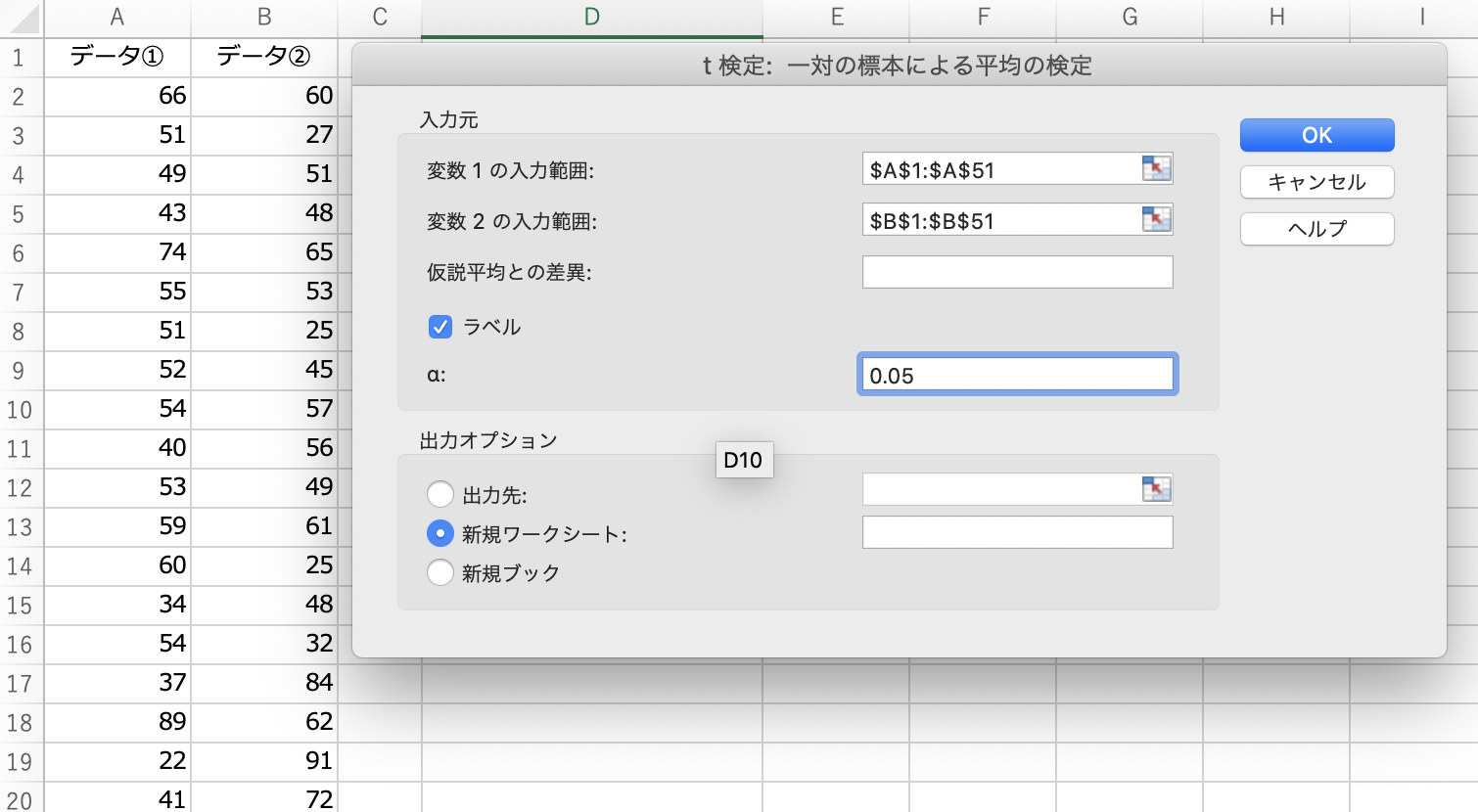
このように、データの範囲と有意水準を指定します。
（1行目が列の名前なら、[ラベル]にチェックを入れましょう。）
すると・・・

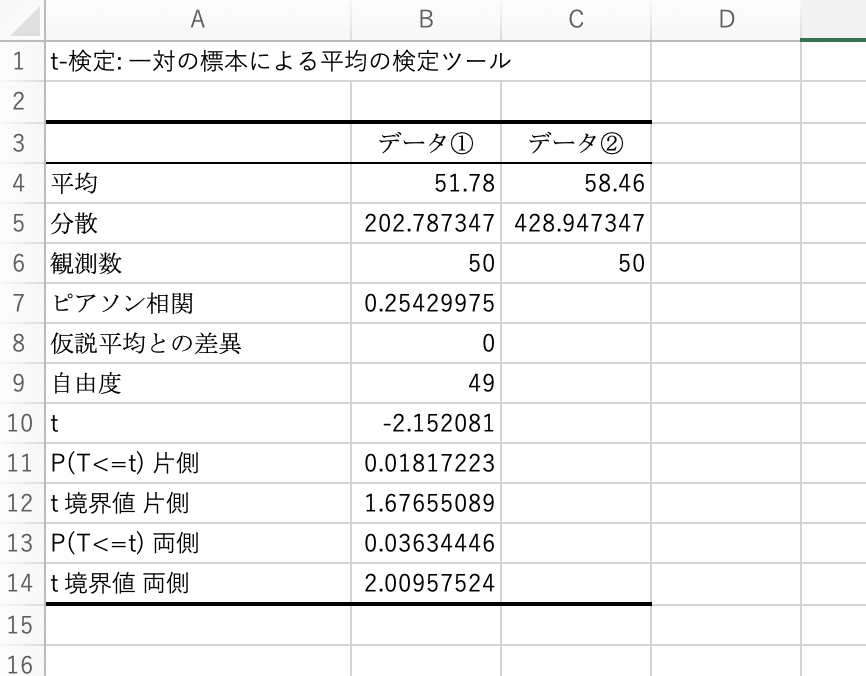
一気にデータの平均・分散や、要素数。それに片側検定の場合のp値と、両側検定の場合のp値などが一気に得られました。
関数で実行した場合と、同じ結果が得られていることが確認できるかと思います。

このように、「データ分析」機能を用いてt検定する方法もあります。

さいごに

もう一度確認すると、まずは

を確認し、これが満たされるのならば、

これらを決定しておけば、もうt検定の準備は万端です。
あとはお好きな方法で分析をしてください。

t検定は非常に利用範囲が広い手法です。
しかし正しく前提条件を決定して、そして正しく結果を評価するようにしないと意味のない分析になってしまいますので、留意しましょう。