「相関係数」を正しく理解しよう

「相関」とは、ある2つのデータが互いにどれほど影響を及ぼしているかを表す指標です。

例えば、ある売店において、「入り口から陳列棚までの距離」と「その商品の売上数」に相関関係があることが分かったとします。
そうすると、売りたい商品は入り口付近に揃えたほうが店の売上が上がりそう、と考えられるわけです。

このように何と何に相関があるのかが分かると、その後の具体的なアクションに繋がります。
ですが、相関分析は、きちんとその意味を理解して正しく行わなければ判断を誤ってしまいます。

今回は、相関分析の考え方、注意点などを踏まえて、Excelにおける相関分析の計算方法をご紹介します。

相関の強さを数値で表す「相関係数」

まず、「相関」には2種類あります。
1つは「一方が上がれば、他方も上がる」という「正の相関」。
もう1つは、「一方が上がれば、他方は下がる」という「負の相関」です。

「正の相関」があるならば「相関係数」はプラス。「負の相関」があるならば「相関係数」はマイナス。まったく相関がないと、相関係数は0になります。
そして、相関係数は必ず-1〜1の値になります。

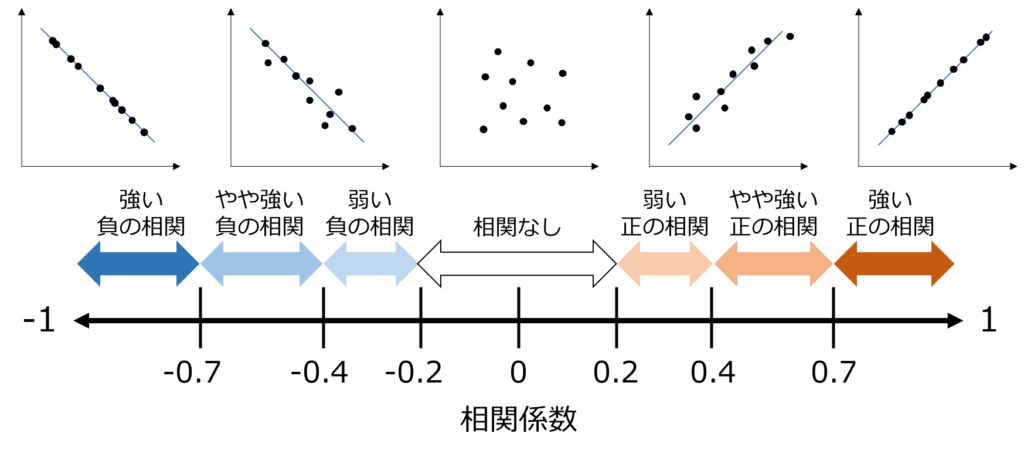
より直線に近ければ、正の相関なら0.8〜0.9などという大きい値になり、負の相関なら-0.8〜-0.9などという小さい値になります。
このように直線に近ければ近いほど、相関係数の絶対値は大きくなります。

つまり「相関係数」とは、グラフの点々が直線にどれだけ近いか？という指標です。

相関係数の求め方

さて、上記のポイントを押さえたら、実際に相関係数を計算してみましょう。

Excelで求める場合

相関係数を求める関数として、以下のCORREL関数が使えます。

=CORREL(配列1,配列2)

配列1と配列2は同じ要素数でなければいけません。

また、列が幾つもあって、それらのすべての相関を求めたい時があります。
そういった場合は、「データ分析」機能の「相関分析」オプションを使いましょう。

参考：Excelで分析ツールを読み込む

上記に習って設定すると、選択した行のすべての組み合わせにおいてその相関係数を計算してくれます。
同時にたくさんの相関を求めたい場合はこちらを使うと良いでしょう。

Pythonで求める場合

Pythonを使うと、図で分かりやすい相関分析をすることが出来ます。
こちらは別記事として整理しています。

Pythonで相関係数を求めて可視化する方法

相関係数を信じる前に・・・

さて、上記のように、相関係数は簡単に計算できます。
しかし、ここからが大切なのですが、そうやって計算された相関係数を、何も考えず鵜呑みにしてはいけません。
相関係数を計算したら、以下のような観点のチェックを怠らないでください。

データ数は充分か？

これはどんな分析においても大切なことですが、そもそもデータ数が少ないと偶然に相関が出てしまう可能性が上がるので、その相関係数を当てにしてしまうことは危険です。

例えば、以下の記事は面白い一例です。
https://togetter.com/li/1119318

どうも、ニコラス・ケイジの映画出演数と、溺死者数に強い相関があるらしいです・・・。
確かに、グラフだけ見ればそのように見えます。

では、ニコラス・ケイジを映画に出演させなければ溺死者数は減るのでしょうか?
・・・まあ普通に考えればそんな訳ありません。

これはただの偶然で相関が出てしまっているのですね。これはデータ数が11と少ないことが要因でしょう。
このように、データが少ないと、偶然で相関が出てしまう確率がグッと上がってしまいます。

極端な話、データが2つしかなければ必ず相関係数は1か-1になります。
2点をぴったり通る直線はいつでも引けてしまいますので。（点が真横or真縦の場合は相関係数は計算不可能になります）

データ数は多ければ多いほど良いのは確かですが、しかし具体的に幾つ以上あれば完璧！という指標はありません。
データをどうしても少数しか集められない場合は、相関係数は参考値程度に捉えたほうが良いでしょう。

ちなみに私の感覚としては、最低でも30データ程度は欲しいかなとと考えています。

極端な外れ値は無いか？

実は相関が無いのに、極端な値が少数存在するせいで相関が出てしまうという場合があります。
逆に、相関があるのに無くなってしまう場合もあります。

それは、データが以下のようになっている場合です。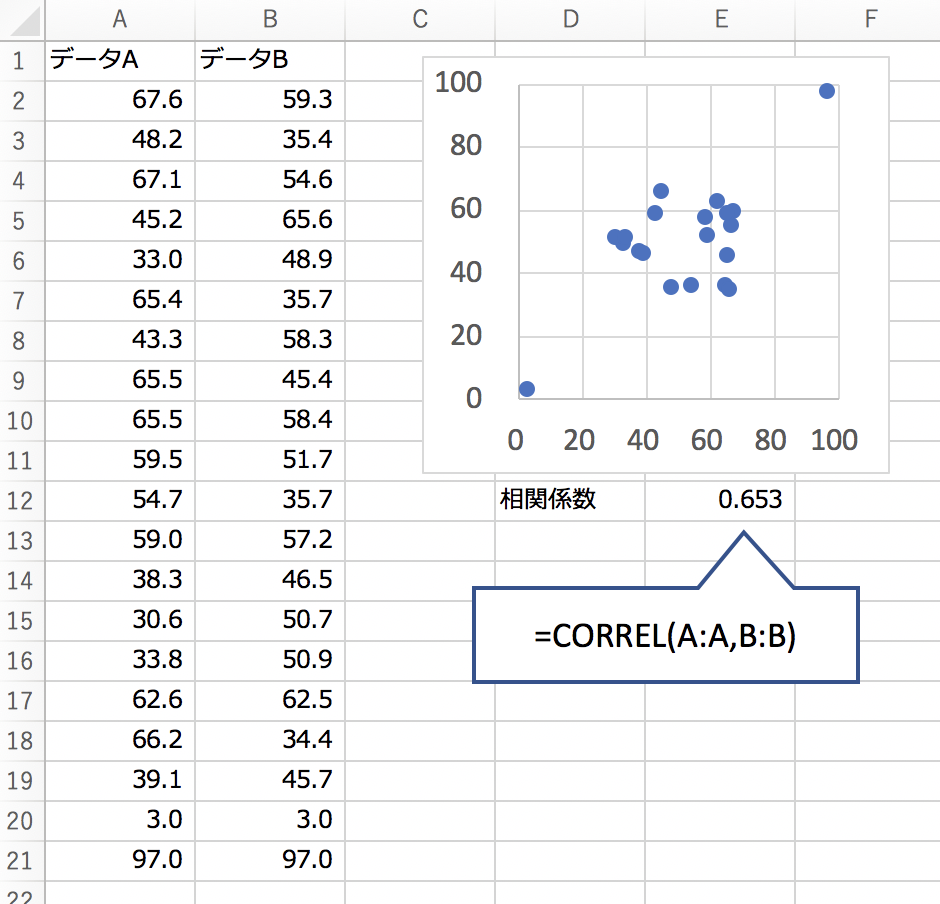

極端な2つの点が無ければほぼ無相関のようです。
しかし、この極端な2点のせいで0.6以上の相関が出ているようです。
現に、この2点を取ってみると、相関係数は-0.008になってしまいました。

これは「相関がある」訳じゃなくて、単に「極端なデータがある」だけのようです。
しかし、相関係数だけで結果を判断してしまうと、こういった状況に気づけません。
きちんと散布図を書くことによって見えてくるものもあります。

こんな記事もありました。
https://togetter.com/li/739464

極端なデータが数個あるだけで、ほとんどのデータは団子状態です。
それなのに「相関がある！」と断じてしまっている記事にツッコミが入っているものですね。
何にせよ、一度データをグラフ化してみて、「この相関係数は意味のある値なのか」を考えることは大切です。
まあ、上の記事ではグラフ化した挙げ句に判断を間違えているので、また別問題かもしれませんが・・・。

実は曲線関係ではないか?

相関分析は、ある要素とある要素に「直線関係があるかどうか」しか分かりません。
つまり、曲線の関係性は全く分かりません。

例えば、以下のようなデータがあったとします。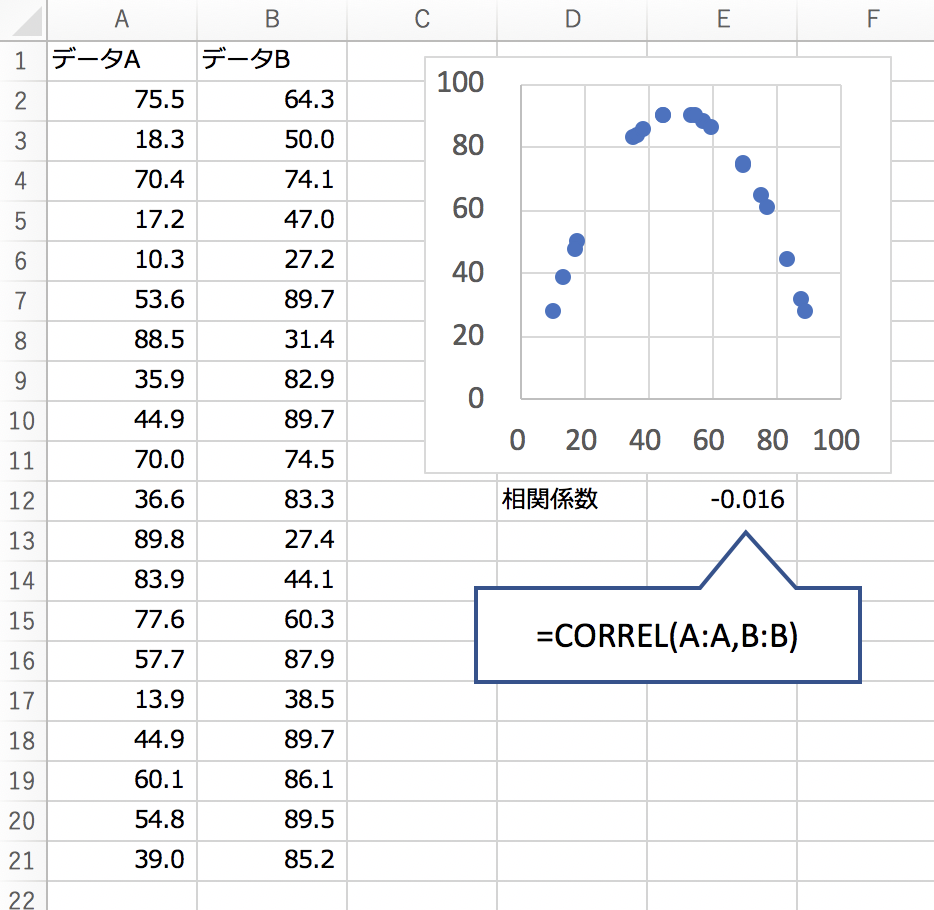

相関係数は-0.016なので、相関は無いようです。
・・・が、どう見ても二次関数のような形状になっています。

これには「曲線関係」という素晴らしい関係性があるのですが、通常の相関分析ではそれに気が付けない訳です。
この、「実は曲線関係」といった状況を発見するためにも、具体的にグラフを書いてみることが大切と分かります。

見せかけの相関ではないか?

例えば、「血圧の高さ」と「年収」には正の相関があるとされています。
これだけだと少々驚きますが、実は「年齢が上がるほど血圧が上がる」「年齢が上がるほど年収が上がる」というだけで、血圧と年収に直接的な因果関係は無いと。
実は因果関係にあったのは「年齢と血圧」と「年齢と年収」だったのですね。

・・・それに気づかず相関分析の結果を鵜呑みにすると、「血圧を上げれば年収が上がるのか！」という判断になってしまいます。
これを「見せかけの相関」、または「疑似相関」「錯誤相関」などとも呼ばれます。
「相関が高い」ことは「因果関係があること」と必ず結びつく訳ではない事に注意してください。

この問題はグラフを書いても分かりませんので、きちんと頭で考える必要があります。

データは正規分布と考えられるか？

最後に数学的な話となりますが、比較する2つのデータが、いずれも正規分布に従っている事が分かっていないと、通常の相関分析は適しません。
そのような場合には「スピアマンの相関係数」「ケンドールの相関係数」という別の指標がありますので、そちらを適用する方がいいかもしれません。
(今まで話してきた一般的な相関係数は「ピアソンの相関係数」と言います。)