多クラス分類における混同行列と、その性能評価指標について整理します。
2クラス分類とは、ある動物の画像が「ネコか、ネコ以外か」に分類するような2択問題を解くもの。
それに対し、多クラス分類とは、ある動物の画像が「一体何の動物なのか」を推測するような、n択問題を解くものです。

多クラス分類の混同行列
ここでは例題として、ある動物の画像が、ネコなのか、イヌなのか、ウマなのかという3択問題を解かせるAIを考えてみます。
この時、例えば「ネコを判別できなかった」という結果は「ネコをイヌと判別してしまった」or「ネコをウマと判別してしまった」という2パターン考えられます。どちらに間違えてしまったのかという情報は大切なので、それらが分かるような混同行列を作ることになります。
この例では、混同行列は以下のように、3×3のサイズのものとなります。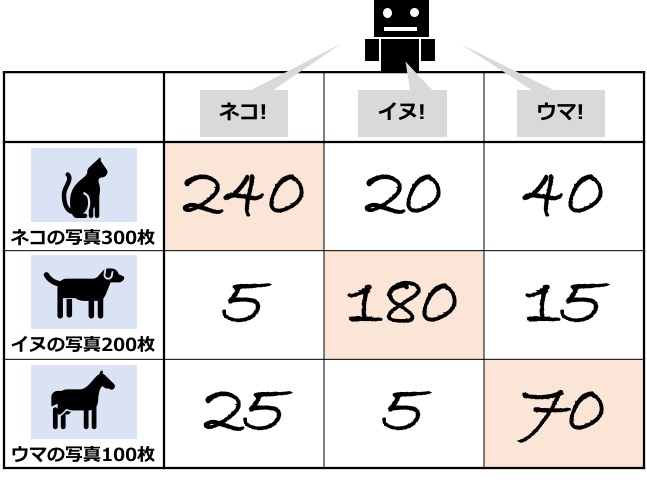
こう書くと、「ネコをイヌと判別してしまった」枚数は20枚、「ネコをウマと判別してしまった」枚数は40枚と分かります。
混同行列のサイズが大きくなるだけで、表の意味は2クラス分類とほとんど変わりません。
ただ、多クラス分類特有の評価指標が幾つかありますので、それをご紹介します。
多クラス分類の評価指標
多クラス分類問題であっても、「正解率」に関しては、クラス数の多さ(混同行列の大きさ)に関わらず、ただ1つだけ計算されます。
それに対して「再現率」「適合率」「F値」はクラスそれぞれについて計算されるので、クラスごとの結果を1つにまとめる必要があります。
(これらの用語の意味については2クラス分類の記事をご参照ください。)
正解率
最も単純な指標で、全ての評価データのうちの正解している数です。
クラスごとの枚数の差が小さければ大きな問題は無いのですが、
「ネコの評価データは10000枚あるのにイヌの評価データが100枚しかない」と言ったように、クラスごとのデータ数に差がある時は、ほとんどネコの結果に引っ張られてしまうので、向きません。
再現率の平均(マクロ平均再現率)
クラスごとに再現率を計算し、それらを単純に平均したものです。
単純平均した値の事を「マクロ平均」と呼ぶことから、「マクロ平均再現率」と書かれることもあります。
こちらはクラスごとに計算するので、先程のようなクラスごとのデータ数の差はあまり気にする必要はありません。
適合率の平均(マクロ平均適合率)
クラスごとに適合率を計算し、それらを単純に平均したものです。
上記同様、こちらも「マクロ平均」ですので、「マクロ平均適合率」と書かれることもあります。
ひとつ注意は、一般的に「平均適合率」という言い方をすると、Average Precisionという別の指標を指します。
そのため、ここでは「適合率の平均」という書き方にしています。
F値の平均(マクロ平均F値)
平均F値は、調べる限り2つの定義があるようです。
1つ目は、クラスごとにF値を計算し、それらを単純に平均したもの。
2つ目は、「再現率の平均」と「適合率の平均」の調和平均を取ったもの。
以上2つの定義が見受けられるのですが、一概にどちらが優れているとは言えません。
なので、どちらの計算方法を用いるかをきちんと定義した上で使用しましょう。
ちなみに、「マクロ平均〜」に対して「マイクロ平均再現率」「マイクロ平均適合率」「マイクロ平均F値」という概念もありますが、多クラス混同行列においては、これらの値は全て「正解率」と一致しますので、除外しています。
整理
以上を1つに整理した図が以下となります。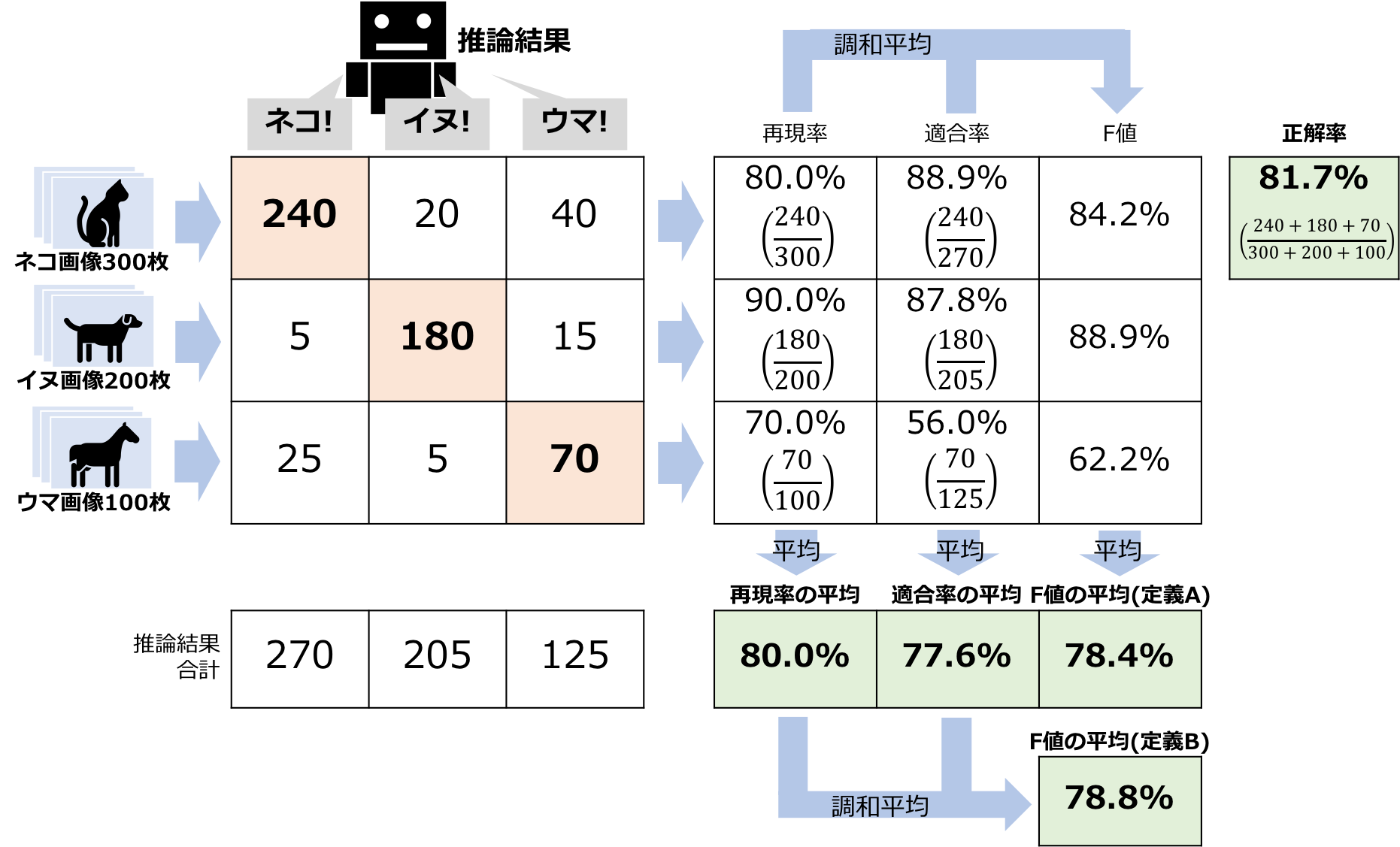
結局、きちんと検討する時はクラスごとの再現率・適合率をすべて書き並べて総合的に考えるのが一番良かったりしますが、その性能を一言ばしーん!と言い表すには何かしらその評価指標を決定しなければなりません。
それが上記4つのいずれかなのか、はたまた4つのいずれも適さないのか。
その検討の一助となれば幸いです。
Excelで多クラス混同行列を作る
最後に、おまけとしてエクセルの関数だけで混同行列の性能指標を計算してみます。
関数をコピペするだけで使えますので、ご活用ください。
混同行列の作成
まずは混同行列を左上から作成してください。
A列と1行目にはクラス名の記載が必要です。
以下、一例です。
関数の貼り付け
1行目には評価指標名称、2行目には以下の関数をコピペし、行列の右側に順番に貼り付けてください。
クラス数(行列のサイズ)は幾つでも問題ありません。
正解数
再現率
適合率
F値
正解率
平均再現率
平均適合率
平均F値(定義A)
平均F値(定義B)
すべてコピペすると以下のようになります。
関数についての細かい説明は致しませんが、相対セル参照やoffset関数を活用して、どんなサイズの行列にも対応できるように調整してあります。
全ての行への反映
「正解数」「再現率」「適合率」「F値」はクラスごとに計算されますので、縦列へもコピーが必要です。
2列目の上記4セルを選択し、右下の小さな正方形をダブルクリックすれば縦列にコピーされます。
正しく計算が行われると以下のようになります。
整形
あとは、見やすいように表示をお好きに修正してください。
以下、一例です。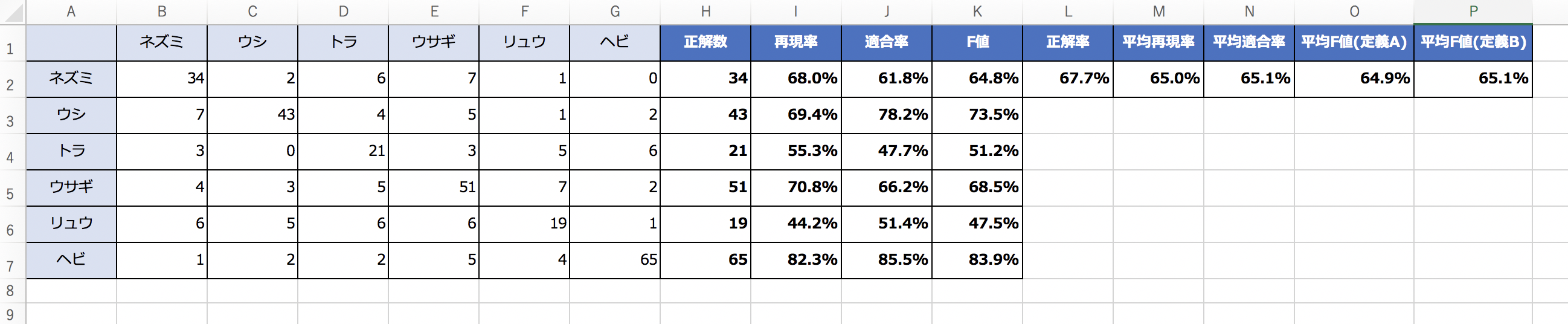
これで、Excelで多クラス混同行列の様々な評価指標が算出されました。
Pythonを扱える場合は、もっと簡単に計算できますので以下の記事をご参照ください。