2024年11月27日 / 最終更新日 : 2024年12月2日 Takuma Nishimaki 学習用記事

AHP(階層分析法)の理論と、その実行方法【意思決定理論】

意思決定理論のひとつ、AHP（階層分析法：Analytic Hierarchy Process）の方法論と、それをExcelやPythonで実行する方法を紹介します。
AHPを理解すれば、就職先選び、購入する製品選び、お店選び、投資先選び、、、など様々な「意思決定」が必要な場面で、迷わずあなたにとっての最適解を理論的に知ることができます。

AHPとは

「次に購入するPCはWindowsにするか、Macにするか」「今日の夕飯は和食にするか、洋食にするか、中華にするか」・・・
などなど、私たちは1日に何回も意思決定を迫られています。
こういったレベルの悩みであれば「えいや」と決めてしまってもいいのでしょうが、「投資する企業はどこが良いか」「就職先はどこが良いか」・・・などなど、易々と決められない事も多くあります。

そこで、AHPを用いると、複雑な状況下においても最適な選択を数学的に導き出すことができます。

AHPを行うのに必要な情報は2つ。1つは何に悩んでいるかの「選択肢」。もう1つは意思決定を行うのに必要な「判断基準」です。
「選択肢」というのは単純に、例えば転職先で悩んでいるなら悩んでいる対象の「企業A」「企業B」「企業C」・・・ということになります。
「判断基準」というのは、会社選びなら例えば「給料」「忙しさ」「やりがい」「テレワーク率」・・・といった項目になります。
判断基準は状況によって何を選ぶのかは変わるでしょうが、「迷う原因」になっている項目を選びましょう。

さて、これらの項目を洗い出した後。ここがAHPの最大の特徴なのですが、「判断基準ごとの、1対1比較」を繰り返していきます。
上記の例で言えば「給料の観点では、会社Aは会社Bと比べてどのくらい良いだろうか？」というように、問題を細分化して判断しやすくします。

つまり選択肢も多い、判断基準も多い、という状態だからこそ迷うわけです。
そこで「1つの大きな問題」を「複数の小さな問題」分解し、最後にその結果を統合することで最終結果を導き出す、AHPはそんな方法です。

AHPの実行

1対1比較の実施

では、「小さな複数の問題」はどのように評価していくのでしょうか。
この「〇〇の観点では、AはBと比べてどのくらい良いだろうか？」という「小さな問題」の評価ですが、この判断は一般的に下記の点数表に従って行います。

点数	意味
9	Aがかなり良い
7	Aが良い
5	Aがまあまあ良い
3	Aがわずかに良い
1	AとBは同等
1/3	Bがわずかに良い
1/5	Bがまあまあ良い
1/7	Bが良い
1/9	Bがかなり良い

例えば「給料の観点では、会社Aは会社Bと比べてどのくらい良いだろうか？」と考え、Aの方がわずかに良いならば3点をつけます。
そしてこの時、「給料の観点では、会社Bは会社Aと比べてどのくらい良いだろうか？」という逆の問題の点数は必然的に1/3に決まります。
Aから見たBが3倍なら、Bから見たAは逆数の1/3倍という訳ですね。

ちなみにこの表は一例であり、9段階が細かすぎると思えば7段階でも5段階でも良いです。
点数も、1,3,5,7…でなくても問題ありません。
が、この点数付けが最も広く使われているため、特にこだわりがなければこの表に則れば良いでしょう。

1対1比較の統合

この1対1比較を繰り返していくわけですが、この結果は判断基準ごとに下記のようなマトリックス形式で表現していきます。

【「給料」についての比較】

	企業A	企業B	企業C
企業A	$1$	$3$	$5$
企業B	$\dfrac{1}{3}$	$1$	$3$
企業C	$\dfrac{1}{5}$	$\dfrac{1}{3}$	$1$

左上から右下へ向かう対角成分はすべて「同じもの同士の比較」なので1が入ります。
例えば企業Bにおいては、企業Bから見て「企業Aよりは少し悪いから1/3」「企業Cよりは少し良いから3」というように値を入れます。
そして対角線に対して対象の位置にあるものは「3」と「1/3」のように、必ず逆数が入ります。ここは先述した通り。

つまり3社で悩んでいるならば、表のマスは9つですが結局「企業A vs B」「企業A vs C」「企業B vs C」の3つの評価をすればOKです。
数学的に書くならば、N個の選択肢で悩んでいるなら ${}_N \mathrm{C}_2$ 回の比較が必要、というわけです。

補足

1対1評価では評価の整合性が保たれるようにご注意ください。
例えば「企業A vs B」でAが優位。「企業A vs C」でCが優位と評価した場合、B＜A＜Cという関係性になります。それなのに、「会社B vs C」の評価でBが優位、としたら整合性が取れていないことになります。
ただし評価値の整合性が取れているのか計算で確認する方法もありますので、そちらは次節で紹介します。

このようにすると、判断基準ごとに下記のような表が出来上がっていきます。

【「忙しさ」についての比較】

	企業A	企業B	企業C
企業A	$1$	$7$	$\dfrac{1}{3}$
企業B	$\dfrac{1}{7}$	$1$	$\dfrac{1}{9}$
企業C	$3$	$9$	$1$

【「やりがい」についての比較】

	企業A	企業B	企業C
企業A	$1$	$\dfrac{1}{3}$	$3$
企業B	$3$	$1$	$5$
企業C	$\dfrac{1}{3}$	$\dfrac{1}{5}$	$1$

【「テレワーク率」についての比較】

	企業A	企業B	企業C
企業A	$1$	$\dfrac{1}{5}$	$\dfrac{1}{7}$
企業B	$5$	$1$	$\dfrac{1}{3}$
企業C	$7$	$3$	$1$

このようにして「判断基準ごとの、選択肢の1対1比較」が完了しました。
そしてもう1つ、「判断基準の1対1比較」も実施します。今の例で言えば「給料」「忙しさ」「やりがい」「テレワーク率」の4つの優先度を決めると言うことです。
こちらも同様にマトリックスを作り下記のように評価していきます。

【判断基準の比較】

	給料	忙しさ	やりがい	テレワーク率
給料	$1$	$\dfrac{1}{3}$	$1$	$3$
忙しさ	$3$	$1$	$3$	$9$
やりがい	$1$	$\dfrac{1}{3}$	$1$	$5$
テレワーク率	$\dfrac{1}{3}$	$\dfrac{1}{9}$	$\dfrac{1}{5}$	$1$

これらの表を用いて、総合的な「あなたにとっての最適な選択」を調べていきます。
その方法として大きく「固有値法」「幾何平均法」という2種類のやり方がありますので、順に見ていきましょう。
詳しくは次の章で解説しますが、ざっくり先に述べておくと、固有値法は幾何平均法と比べて、数学的に正確ですが、その分理解が難しい方法となりです。
とにかくAHPをざっくり理解したい、という場合は「幾何平均法」の方をご覧いただくと良いかと思います。

固有値法による評価方法

さて、固有値法では、先ほど作成した表を行列式とみなします。そして、この行列を $A$ と置いた時の $Aw = \lambda w$ を満たす固有ベクトル $\lambda$ を求めます。

ここで、要素が3つなら固有値も3つ出ますが、その中での最大固有値と、それに対応する固有ベクトルに着目します。
これは主成分分析と同様、最大固有値に対応する固有ベクトルは、行列全体の情報を最もよく集約しているという考えに基づいています。

最大固有値・固有ベクトルの計算はこの行列は特性方程式 $\det(A-\lambda I) = 0$ 　(※ $I$ は単位行列) を解けば求まりますが、基本的に手計算やExcelでは難しいので、例えば下記のようにPythonなどで行うのが現実的でしょう。

import numpy as np

# ペアワイズ比較行列Aの定義

A = np.array([[1, 3, 5],

[1/3, 1, 3],

[1/5, 1/3, 1]])

# 固有値と固有ベクトルの計算

eigenvalues, eigenvectors = np.linalg.eig(A)

# 最大固有値のインデックスを取得

max_index = np.argmax(np.real(eigenvalues))

# 最大固有値と対応する固有ベクトルを取得

lambda_max = np.real(eigenvalues[max_index])

eigenvector_max = np.real(eigenvectors[:, max_index])

print("最大固有値（λ_max）：", lambda_max)

print("固有ベクトル：", eigenvector_max)

# 重みの計算

weights = eigenvector_max / np.sum(eigenvector_max)

print("重み（正規化した固有ベクトル）：", weights)

最後の重み計算ですが、固有ベクトルの値は解釈性の向上のため、固有ベクトルは通常合計1になるように正規化します。あくまで相対的な数字の大きさを見るだけですので正規化しても問題ありません。

このようにして求められた最大固有値（ $\lambda_{max}$ と表記します）に対応する固有ベクトルの各成分が、この評価軸における比較対象の相対的な重要度と解釈されます。
ちなみに数値計算の都合上、結果に虚数部が含まれる可能性がありますが、「ペロン＝フロベニウスの定理」により、「非負の正方行列はただ一つの実数である最大固有値が存在し、それに対応する固有ベクトルの各成分は厳密に正である」ということが約束されます。つまりAHPの計算で使用する部分は必ず実数解が得られます。

補足

上記スクリプトですが、コンピュータの丸め誤差の影響で虚数が含まれてしまう場合が稀にあるため、念の為np.realを用いて実部のみ取り出しています。
また、固有ベクトルが負の値で出てきてしまう場合がありますが、これもコンピュータ計算の都合です。固有ベクトルは任意のスカラー倍で表現されるため、すべての要素に-1を掛け算したものも固有ベクトルとなりますので、すべての要素が負でも問題ありません。

さて、上記のスクリプトを実行すると、以下のような結果が得られました。

最大固有値（λ_max）： 3.0385110905581736

固有ベクトル： [0.916142 0.37147738 0.1506267 ]

重み（正規化した固有ベクトル）： [0.63698557 0.25828499 0.10472943]

つまり、小数点以下3位で四捨五入すると最大固有値 $\lambda_{max}=3.04$ 　、そしてそれに対応する重みは $(0.64,0.26,0.10)$ と計算されます。
これは「給料の面から見ると、優先度は企業A=約64%、企業B=約26%、企業C=約10%」という解釈となります。

同様に他の評価軸でも重み（重要度）を計算すると下記のようになりました。

忙しさ：企業A=約29%、企業B=約5%、企業C=約66%

やりがい：企業A=約26%、企業B=約64%、企業C=約10%

テレワーク率：企業A=約7%、企業B=約28%、企業C=約65%

また、評価軸ごとの重み計算も行います。行列サイズは異なりますが計算方法は一緒です。こちらも上記の例を用いると、

評価軸：給料=約18%、忙しさ=約55%、やりがい=約21%、テレワーク率=約5%
という結果が得られました。

これらの値を用いて最後に「総合評価」を行なっていきましょう。これは単に上記で計算した重みの加重平均を取っていくことで計算されます。
つまり、「企業Aの総合重要度」は64% * 18% + 29% * 55% + 26% * 21% + 7% * 5% = 約34%です。同様に
「企業Bの総合重要度」は26% * 18% + 5% * 55% + 64% * 21% + 10% * 5% = 約23%
「企業Cの総合重要度」は10% * 18% + 66% * 55% + 10% * 21% + 65% * 5% = 約44%
が得られ、「企業Cの総合重要度」が最も高いという事がわかりました。
同時に次点は企業A、最も良くないのは企業Bという事もわかります。

なおすべての重みが正規化されているならば、この総合評価の合計も必ず1(100%)になることが約束されますので、この数値はそのまま解釈可能です。
固有値法ではこのようにして選択肢の優先順位を評価することができます。

固有値法による入力の整合性の評価

さて、AHPの計算にあたりいくつかの正方行列を作成したかと思います。先述したようにこの行列の値は整合性が取れたものでないといけません。
行列に整合性が取れているかどうか、計算過程で出現した最大固有値 $\lambda_{max}$ の値から下記の通りCI（Consistency Index:一貫性指標）、CR（Consistency Ratio:一貫性比率）を算出することで数学的に検証する事ができます。

$CI=\dfrac{\lambda_{max}-n}{n-1}$

$CR=\dfrac{CI}{RI}$

$n$ は行列の次元数です。

ここで行列が完全に一貫している場合（すべての判断が矛盾なく行われている場合）、その行列はランク1の行列に近づきます。そしてランク1の行列の場合、 $n=\lambda_{max}$ となります。その場合CIの分子は0になるため、CI=0となります。行列に矛盾があればあるほどCIは大きくなります。
また $n-1$ で割ることで行列のサイズに依存しない評価が可能になります。

RI(Random Consistency Index)は「ランダム一貫性指数」と言い、ランダム生成された $n$ 次元の比較行列に対してCIを計算し、それを平均した値です。
つまり $CI/RI$ は、行列が完全ランダムだった場合のCIと比べて、今のCIがどれほど小さいか（行列に一貫性があるか）を示します。

RIについては下記のように既知の値を使用すればOKです。

行列サイズ	3	4	5	6	7	8	9	10
RI	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

そして一般的にこのCRの値が0.1〜0.15以下に収まっていれば、その行列は一貫性が高い、と評価されます。
このCI・CRの計算については下記のように実行できます。

この記事で用いた行列のCRを確認すると、

「給料」についての比較行列：0.033

「忙しさ」についての比較行列：0.069

「やりがい」についての比較行列：0.033

「テレワーク率」についての比較行列：0.056

判断基準の比較行列：0.012

・・・となり、すべての行列の一貫性が保たれていることがわかりました。

幾何平均法による重み付け方法

さて、固有値法は数学的に正確とはいえ、「手法や実行方法が少し難解で、気軽に実行できない」というデメリットがありました。
そこまでの厳密さを求めないのであれば、これから紹介する幾何平均法を用いることをオススメします。
これは比較行列から重要度を計算するプロセスを簡素化し、近似的に最適解を得る方法で、Excelでも実行可能です。

先ほどの行列を1つ再掲します。

【「給料」についての比較】

	企業A	企業B	企業C
企業A	$1$	$3$	$5$
企業B	$\dfrac{1}{3}$	$1$	$3$
企業C	$\dfrac{1}{5}$	$\dfrac{1}{3}$	$1$

固有値法ではこの表を行列に見立てて計算を行いますが、幾何平均法ではその名の通り、企業ごとの幾何平均を計算した値を使用します。
幾何平均というのは、n個の値があった場合「すべての値を掛け算して、そのn乗根を取った値」です。

つまり、企業Aから見ると $1\times3\times5$ の3乗根で、約2.47。
企業Bから見ると $1/3\times1\times3$ の3乗根で、1。
企業Cから見ると $1/5\times1/3\times1$ の3乗根で、約0.41。

これらが「給料」についての各企業のポイントとなります。A＞B＞Cの順番ですね。
このポイントはそのまま理解可能ではありますが、より解釈性を高めるために合計1になるよう正規化します。
上記の例で言えば、すべての値を約2.47+1+約0.41=約3.88で割ることで「給料」面での重要度は企業A=約64%,企業B=約26%,企業C=約10%である、と計算されます。
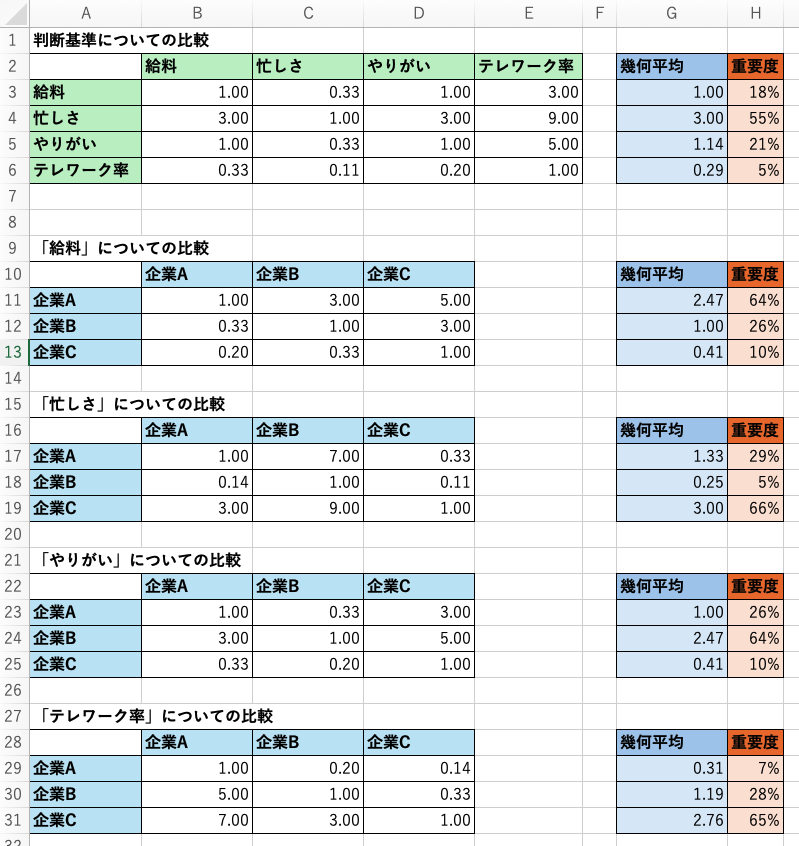
（四捨五入してしまえば固有値法で計算した場合の重要度と同じ数値となっているようです。）

Excelで実施する場合は下図のように表を作成し計算することができます。