以前、回帰分析を用いて気温とアイスクリームの売上の関係について推測しました。

「気温」の情報だけでもなかなか良い推測が出来たようですが、気温だけでなく、もっと色々なデータがあったとしたらどうでしょうか。
例えば天気の情報やアイスクリームの値段の情報など・・・。
さらに精度のよいアイスクリームの売上の推測ができそうです。
そんな訳で、今回は、複数の変数を用いた回帰分析・・・「重回帰分析」をExcelで行ってみます。
理論紹介
変数1つだけで推測する回帰分析を「単回帰分析」、複数の変数で推測する回帰分析を「重回帰分析」と呼びます。
単回帰分析では、求めたいもの(目的変数)が\(y\)で、その計算に使うもの(説明変数)が\(x\)とした時の、\(y=ax+b\)における\(a\)と\(b\)を求めました。
重回帰分析は、説明変数が1つでは無くなるので、単純に\(x\)の項がたくさんになります。
つまり、\(y=a_1 x_1+a_2 x_2+a_3 x_3+…+a_n x_n+b\)における、\(a_1,a_2,a_3,…,a_n\)と\(b\)を求めることが重回帰分析の目的となります。
Excelで重回帰分析を行う
では、以下のような「月平均気温」「値段」「雨」の3つのデータを使って「アイス売上」を予測してみます。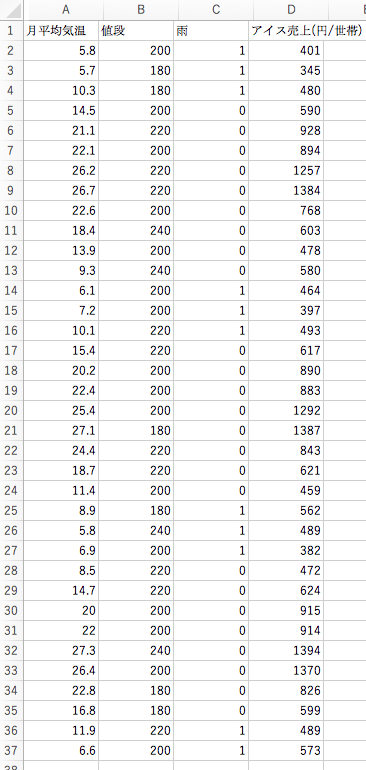
重回帰分析をExcelで行うならば、Excelの「データ分析」機能を使うのが圧倒的に便利です。
初期状態では使えないので、以下の公式サイトを参考にしてデータ分析機能を使えるようにしましょう。
Excelで分析ツールを読み込む
そして、以下のように無事に「データ」タブ内のメニューに「データ分析」が表示されたら、そこから「回帰分析」を選びます。(macの画面ですみません。)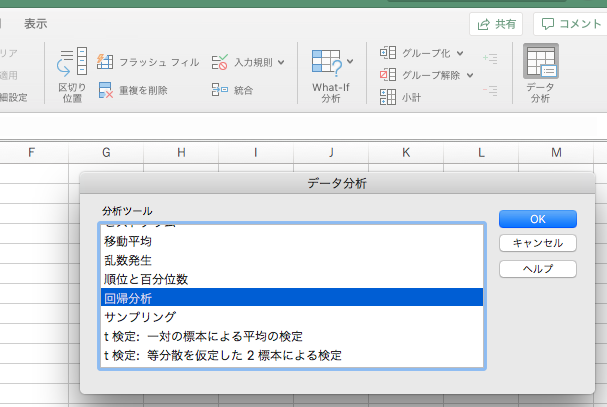
そして、以下のように「入力Y範囲」(=求めたい変数)「入力X範囲」(=求めるのに使う変数)を正しく選択します。
1列目にラベル名(上の例で言うと「月平均気温」「値段」などの列)がある場合は、「ラベル」マークにチェックを入れておきましょう。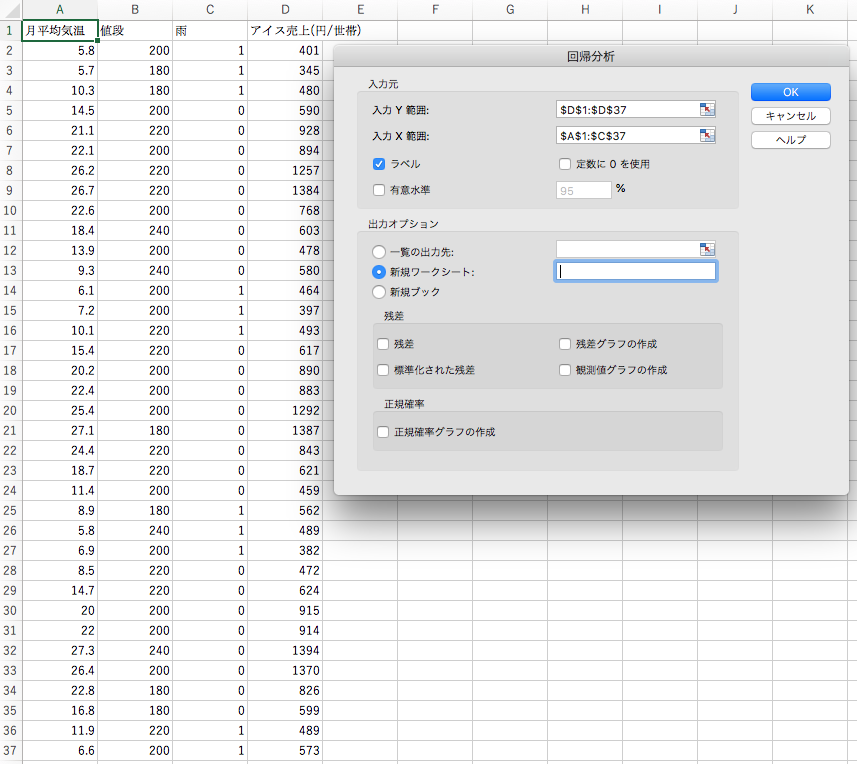
実行すると、別シートに以下のような結果が吐き出されているかと思います。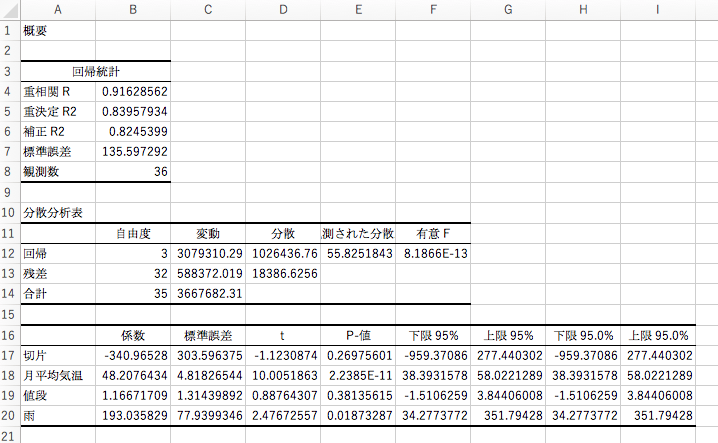
これにて重回帰分析は完成です。
結果の確認
さて、結果を確認してみましょう。
色々と数値が出ていますが、とりあえず確認すべきは一番下の表の「係数」と「P-値」。そしてB5セルの「補正R2」の3つです。
何はともあれ、この3つの数字はチェックしましょう。
係数
係数とは、\(y=a_1 x_1+a_2 x_2+a_3 x_3+…+a_n x_n+b\)における\(a_1,a_2,a_3,…,a_n,b\)の部分です。
今回の例で言えば、「月平均気温」の値を\(x_1\)、「値段」の値を\(x_2\)、「雨」の値を\(x_3\)、とすると、\(y=48.2 x_1+1.2 x_2+193.0 x_3-341.0\)という関係があると読み取ることが出来ます。
P-値
とりあえず存在するデータをすべて活用した推測をしましたが、そもそも使った変数が全て大切な変数(=アイスの売上に関わる変数)かどうかは分かりません。
そこで「P-値」が大切になってきます。(「p値」と表記される事の方が多いので、以降はそう書きます)
p値とは、「その変数がどれだけ大切か」を表す指標で、p値が小さければ小さいほど、その変数は重要と捉えます。
よく用いられる考え方としては「p値が0.05以下」ならその変数は活用し、逆に0.05を超えるならばその変数は使わないようにする方法です。勿論、結果や目的によって0.05という水準を0.01まで下げたり、0.1まで上げたりする場合もありますが、ひとまずは「0.05」を基準と考えて良いでしょう。
ちなみに、「切片」についてはp値の大きさに関わらず必ず使用する必要があります。
今回の例では「月平均気温」は2.2385E-11、つまり\(2.2385\times 10^{-11}\)です。相当小さいので、重要な変数でしょう。
「値段」は0.38135615ですので、重要な変数とは言えなさそうです。
「雨」は0.01873287ですので、重要な変数のようです。
補正R2
単回帰分析では、\(R^2\)値(決定係数)を見れば、その回帰分析の精度を確認できるのでした。それは重回帰分析でも同様です。
しかし、\(R^2\)値というのは、変数が増えれば増えるほど、その値が高くなってしまうという性質があります。
つまり、「売上」にはほとんど関係ない変数が混ざっていても、\(R^2\)値は高くなってしまうわけです。
そこで、重回帰分析では「自由度調整済み\(R^2\)値」を使って回帰分析の性能を測ります。
Excel画面上では「補正R2」と表記されています。
これは、簡単に言うと、通常の\(R^2\)値を、「使う変数が多ければ多いほど、ペナルティを課す」ように調整した指標です。
重回帰分析では通常の\(R^2\)値よりも、こちらの指標を当てにした方が良いでしょう。
今回の例で言えば、約0.825なので、なかなか良い推定が出来ていると考えられます。
より良い予測式を求めて
・・・さて、重回帰分析はこれで出来たわけですが、実は大切なのはここからです。
言ってみれば、ここまでは機械的に誰でも出来る部分です。
ここから、より精度のよい予測をするために試行錯誤するのが、データ分析者の職人技というものです。(少々大げさですが)
先程、変数ごとのp値を確認しました。
すると、「月平均気温」と「雨」は大事だけど、「値段」はあまり関係なさそうだと分かりました。
それならば、いっそ「値段」は初めから除いて計算した方が良いのでは無いでしょうか。
ということで、初めから「値段」の列を消して、改めて重回帰分析を行ってみました。
すると・・・
当たり前ですが、先ほどとは違う結果が得られています。
「月平均気温」の値を\(x_1\)、「雨」の値を\(x_3\)、とすると、\(y=47.6 x_1+178.1 x_3-86.2\)という関係が計算されました。
p値もいずれも0.05を下回っています。
そして、「補正R2」は約0.826ということで、先程の約0.825をほんの僅かに上回っています。
つまり、3変数を使うよりも、無理に「値段」は使わずに2変数だけで推測した方が、より良い推定が出来ていそうですね。
まとめ
このように、重回帰分析は機械的に計算して終わりではなく、人間が正しく結果を解釈する必要があります。
そして、「大切な変数」を見極め、より良い数式は何かと試行錯誤する必要があります。
もちろん、変数選択以外にも、「変なデータが混ざっていないか?」「同じような変数が含まれていないか?」など、考えることは多岐に渡ります。
ExcelでもpythonでもRでも重回帰分析は行なえますが、基本的にコンピュータがやってくれるのは「機械的な計算」だけです。
重回帰分析を行うときは、計算部分をコンピュータに任せるというだけで、あくまでも結果の評価や最終的な意思決定は人間が頭で考えて結論を出すということを忘れないように気をつけてください。