以下は、第40代以降の歴代内閣総理大臣経験者(東條英機〜安倍晋三)の血液型比率を表したグラフと、日本人全体の血液型比率を表したグラフです。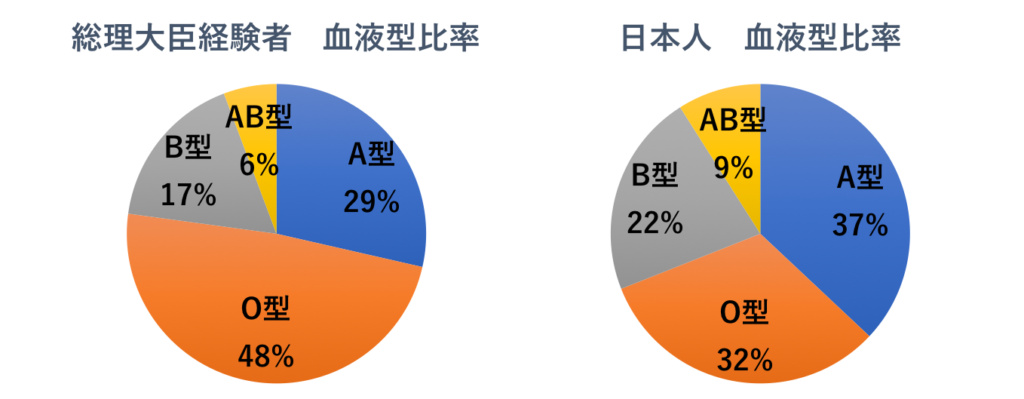
この結果を見て、“内閣総理大臣になるような人物”と、その血液型に関連性があるのかどうか分かるでしょうか?
グラフをそのまま見れば総理大臣にはO型が多いのですが、そもそも日本人にはO型が多い。
人口比率を考えるとB型が多いようにも見える。・・・難しいですね。
そんな時はカイ二乗検定(χ2検定)の出番です。
総理大臣になる人物と血液型が関連するのか、統計学的に調べてみましょう。
カイ二乗検定とは
カイ二乗検定とは、端的に言えば「事象Aと事象Bに関連があるのかどうか」を統計学的に判断する手法です。
今回の例では、“内閣総理大臣になる人物の血液型”と、”日本人の血液型”に関連性があるのかを統計学的に計算することになります。
ちなみに2つの変数は数値で表されるものでなく、「カテゴリー」で表されるものでなくてはいけません。
例えば「年収」というデータは数値なのでそのままでは使えませんが、それを「500万円未満」「500万円以上」とカテゴリー化させれば、カイ二乗検定を適用することができます。
「年代(20代、30代、40代…)」について、「年収500万円未満or以上」の割合に差があるのか比較をする、などですね。
それとウェブマーケティングで用いられるA/Bテストにも、多くの場合カイ二乗検定が用いられています。
「A/Bテスト」というのはインターネットマーケティング等に用いられる手法です。
例えば、ホームページのトップページのデザインを2パターン用意しておいて、それをユーザごとにランダムに表示させ、どちらのデザインにした方がページを最後まで読んでくれる可能性が高いか・・・などをテストする手法のことです。
さて、このように様々な場面で用いられるカイ二乗検定ですが、どのように計算をしているのでしょうか?
実は計算式自体はとてもシンプルなので、簡単にExcelで計算できます。
・・・しかし、きちんと理論を理解して使わなければ正しい判断、正しいアクションに繋げることができません。
ここからはカイ二乗検定がどのような手法なのか、どう行うのかを説明していきます。
カイ二乗検定の理論
カイ二乗検定で行うのは、「期待値」と「実測値」がどれだけ離れているのかを調べることです。
先程の血液型の例で言えば、「総理大臣経験者の血液型比率(実測値)」は「日本人の血液型比率(期待値)」と同じかどうか・・・を調べることになります。
そしてその差が、どれだけ発生しずらいのか(=p値は幾つなのか)を計算するのがカイ二乗検定の焦点になります。
以下のようなイメージです。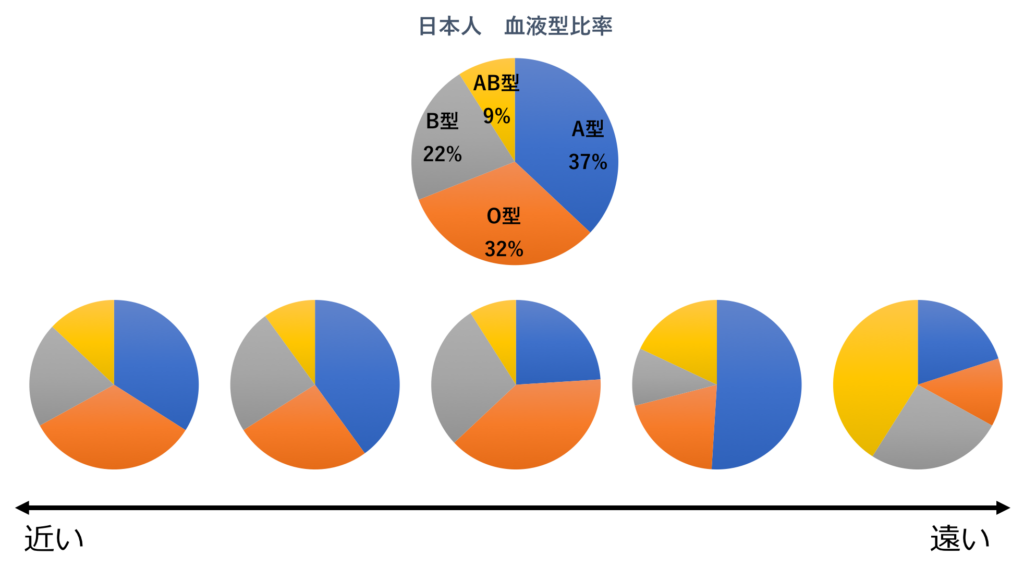
上の円グラフが「日本人の血液型比率(期待値)」で、調べたいデータ(今回で言えば「総理大臣経験者の血液型比率」)がそれに近いかどうか見るわけですね。
左に行けば行くほど、上の円グラフと近いので「血液型と総理大臣経験者に関係はなさそう」となります。
右に行けば行くほど、上の円グラフと離れているので「血液型と総理大臣経験者に関係がありそう」となります。
・・・その離れ具合を、数学的に計算してあげるのがカイ二乗検定です。
(先述したABテストの場合、事象Aと事象Bの期待値を50%/50%として、それと実測値がどれほど離れているのかを見ます。)
計算方法としては、すべての事象における「期待値」「実測値」を書き並べます。
そして、「期待値と実測値の差の2乗」を「期待値」で割った値を全て足し合わせます(今回で言えば、A型・O型・B型・AB型の4つ)。
これを「カイ二乗値」と呼びます。
その値と「カイ二乗分布表」と照らし合わせて、その差がどれだけ起こりやすいのか(p値)を判断することになります。
この辺りの計算はExcelの関数に用意されています。
一般的に、p値が0.05以下だと「2つの事象に差がある」と判断することが多いです。
※統計学では、「差の2乗」という概念がよく出てきます。差の大きさを調べるだけなので2乗する必要性は無いように感じますが、プラスの場合とマイナスの場合で場合分けするのが面倒なので、一律で2乗してプラスに揃えてしまった方が好都合・・・という理由です。
Excelによるカイ二乗検定の実行
では、冒頭の例を用いて、内閣総理大臣になるような人物であることと、その血液型には関連性があるのか?・・・ということをカイ二乗検定で調べてみましょう。
Excelに「実測値」「期待値」のデータを入力します。
そして、以下の関数を適用するだけでp値を計算することができます。
=CHISQ.TEST(実測値の範囲,期待値の範囲)
今回の例だと、以下のようになります。
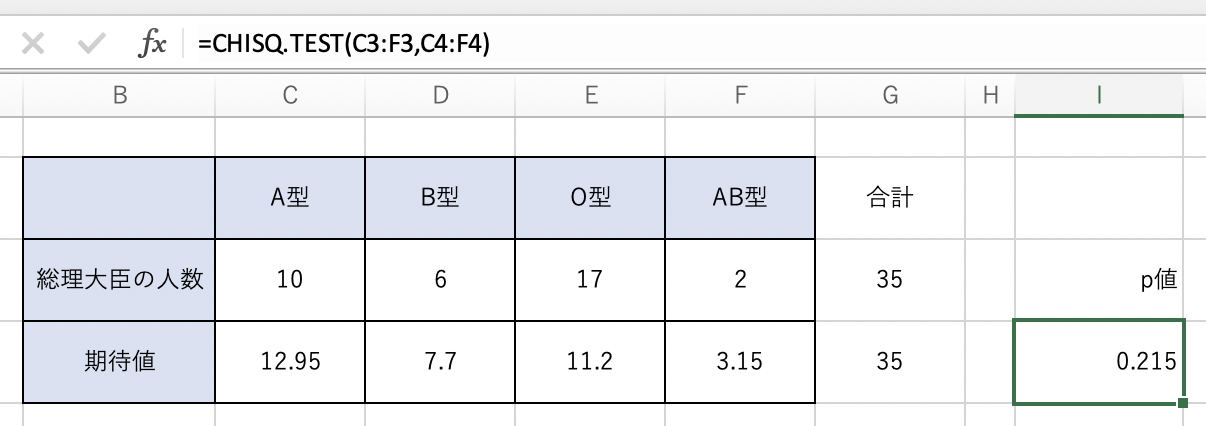
期待値は、今回の対象人数35名を日本人の血液型割合で按分した数値が入っています。
結果を見てみると、p値は0.215です。よって、実測値と期待値には差がないと判断できます。
・・・つまり、「内閣総理大臣になるような人物であることと、その血液型には関連性がある」と分かりました。
まとめ
今回は、「内閣総理大臣になるような人物であることと、その血液型には関連性がない」という結論になりました。
計算自体はシンプルですが、非常に利用範囲の多い検定手法ですので、ぜひ活用して頂ければと思います。