エクセルによる回帰分析

以下は、「2015年から2017年の、月別平均気温(℃)とアイスクリームの売上(円/世帯)」のグラフです。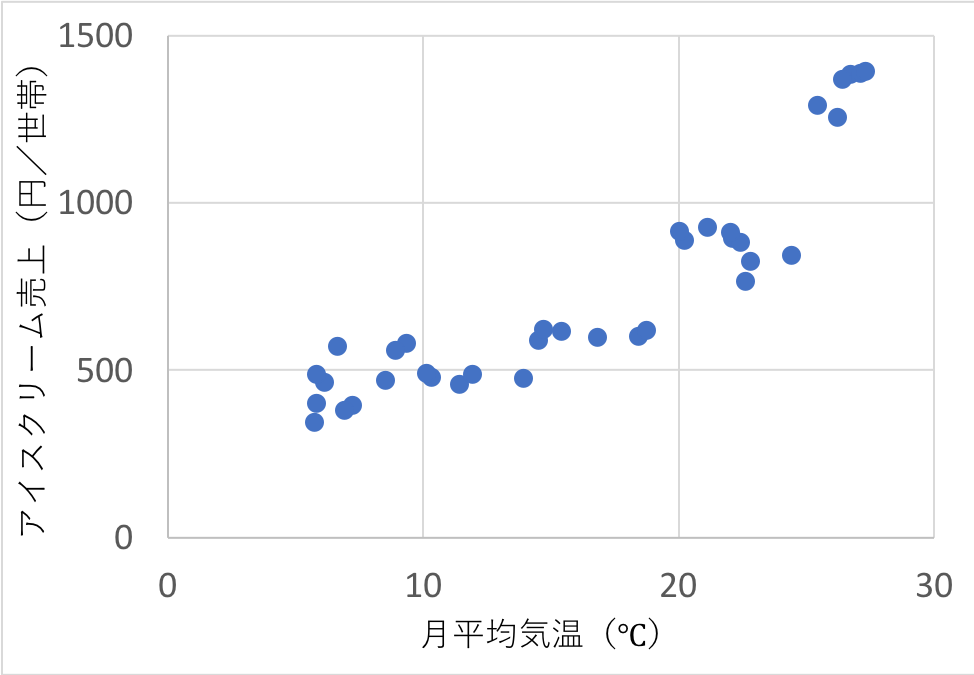

※参考
https://www.icecream.or.jp/biz/data/expenditures.html
http://www.data.jma.go.jp/obd/stats/etrn/view/monthly_s3.php?prec_no=44&block_no=47662

どうも、直線関係があるように見えますね。
パッと見では、アイスクリームの売上は気温を50倍したくらいでしょうか。
・・・しかし、これは人間がグラフを見てなんとなく推測した値なので、もう少しきちんと関係性を表してあげましょう。
ここで、回帰分析の出番です。

回帰分析とは

まず、上述したような「アイスの売上=気温×50」といった関係性を表すものを「予測モデル」と呼びます。
「予測モデル」を作っておくと、気温が分かればアイスクリームの売上がどのくらいになりそうか予測することが出来ます。

このように実際に手元にあるデータを使って「予測モデル」を作り、それを使って未知の結果を推測するという一連の流れはデータ分析の現場においてごく当たり前に行われる事です。
そしてその予測モデル作成の最も基本となる手法、それこそが「回帰分析」です。

ちなみに今回は「気温」のみでアイスの売上を予測していますが、特に変数は1つである必要はありません。
「湿度」のデータを追加したり、「天気」という数値でないデータを含めることもできます。
また、直線関係に限らず使えます。

・・・が、「1変数かつ直線関係」が回帰分析の基本型となりますので、本記事ではそれに絞ってお話します。

適切な近似曲線を選んでいますか？

簡単に理論説明

傾きと切片の計算

回帰分析で行いたいことは簡単で、以下のように全ての点からの距離の合計が小さくなるような直線を引くことです。
ただし、距離はそのまま足し算するのではなく、距離を2乗したものを足します。こうすると、距離がプラスのものも、マイナスのものも、全てプラスに揃うので計算しやすくなります。

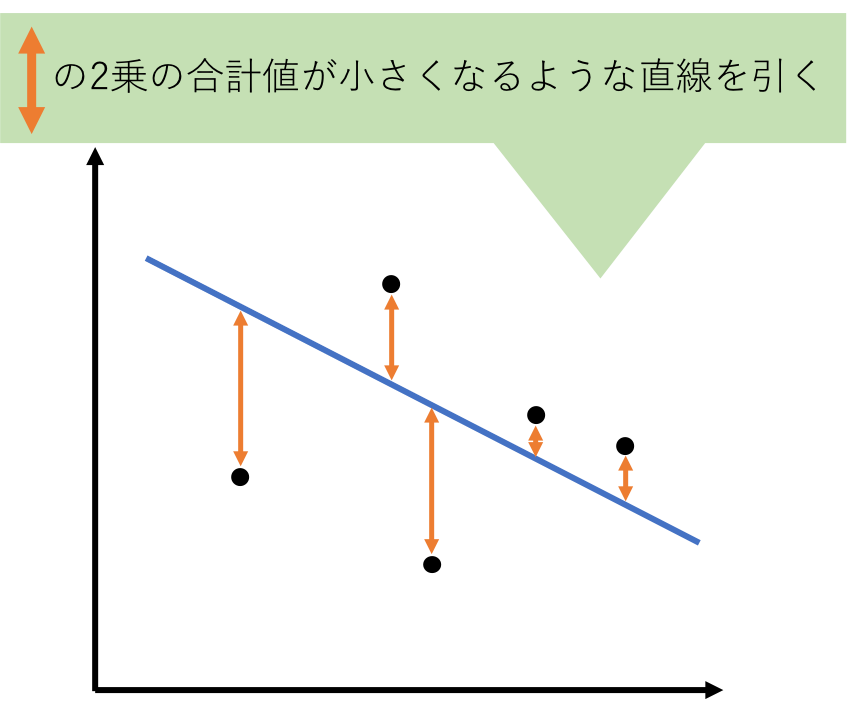
相関分析と似ていますね。
ただ、相関分析は単に「どれほど直線関係に近いか」を見ていただけなのに対し、回帰分析はその直線の式まで求めます。
すなわち１次関数y=ax+bにおける傾きa、切片bを求めるわけです。

これは闇雲に何本も直線を引いてみて、その中で最も距離の合計が小さいものを選ぶわけではなく、きちんと正確な求め方があります。
今回その詳細の説明までは行いませんが、傾きは(XとYの共分散)÷(Xの分散)で求めます。
切片は、先に計算した傾きを持ち、かつ(xの平均,yの平均)を通る直線を調べることで求めます。

決定係数(R²値)の計算

「決定係数(R²値)」というのは回帰分析の精度を表します。
直線を引くのは良いものの、その直線がいい感じに全ての点の場所と近いのか、そうでないのかによって、
一次関数の式の信頼度が変わります。下のようなイメージです。

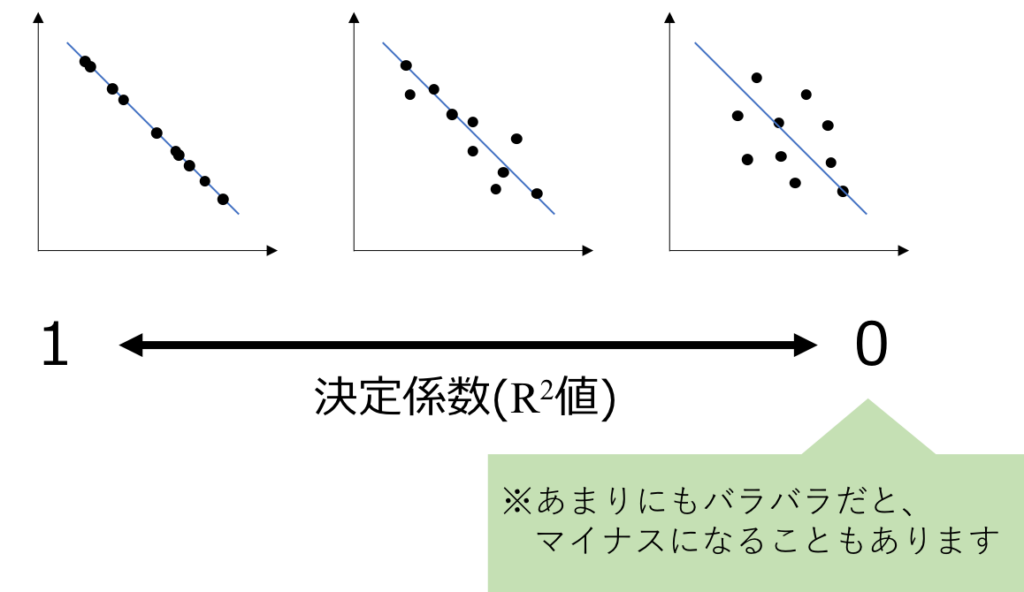
決定係数が1に近い方が精度が高いと見なせます。
ただし、後述しますが、データ数が少ないと偶然に決定係数が高くなってしまう可能性が高くなりますので注意しましょう。

Excelで回帰分析を行う

さて、Excelで回帰分析を実行するのはそこまで難しくありません。
何はともあれ、「アイスの売上」と「平均気温」をずらーっと並べます。

あとは、以下の表に記載した関数を使うだけで簡単に傾き・切片・決定係数が計算できます。
左がy、すなわち「求めたいもの」。今回で言えば「アイスの売上」です。
右がx、すなわち「目的のものを求めるのに使う変数」。今回で言えば「平均気温」・・・の順番になるようにしてください。
この順番を間違えると正しい計算結果が得られません。

傾き(a)	=SLOPE(yの範囲,xの範囲)
切片(b)	=INTERCEPT(yの範囲,xの範囲)
決定係数(R²)	=RSQ(yの範囲,xの範囲)

もう1つ、視覚的に１次関数を表示させることもできます。
まずはグラフで、先程書き並べたデータを選択して「散布図」を書きます。

その後、グラフを選択して、[グラフ要素を追加]>[近似曲線]>[線形予測]を選ぶと、グラフ上に直線が引けます。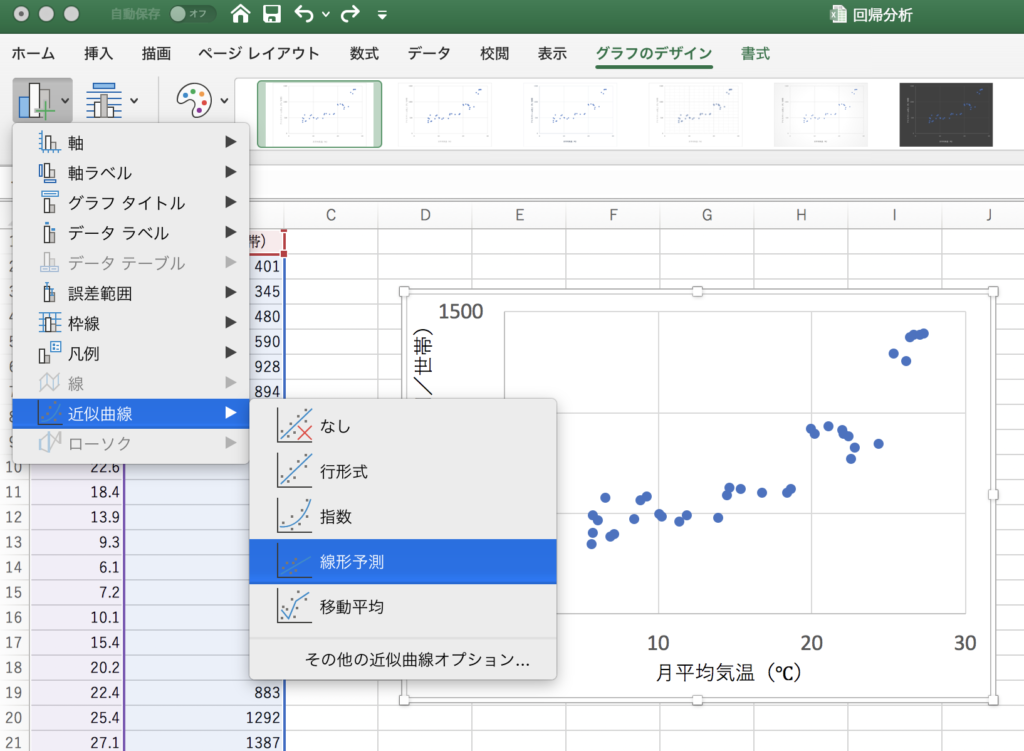

その後、書かれた直線を右クリックして[近似曲線の書式設定]を選ぶと右側にメニューが出てきて、その下部の「グラフに数式を表示する」「グラフにR-2値を表示する」のチェックボックスを入れれば数式や決定係数を表示することができます。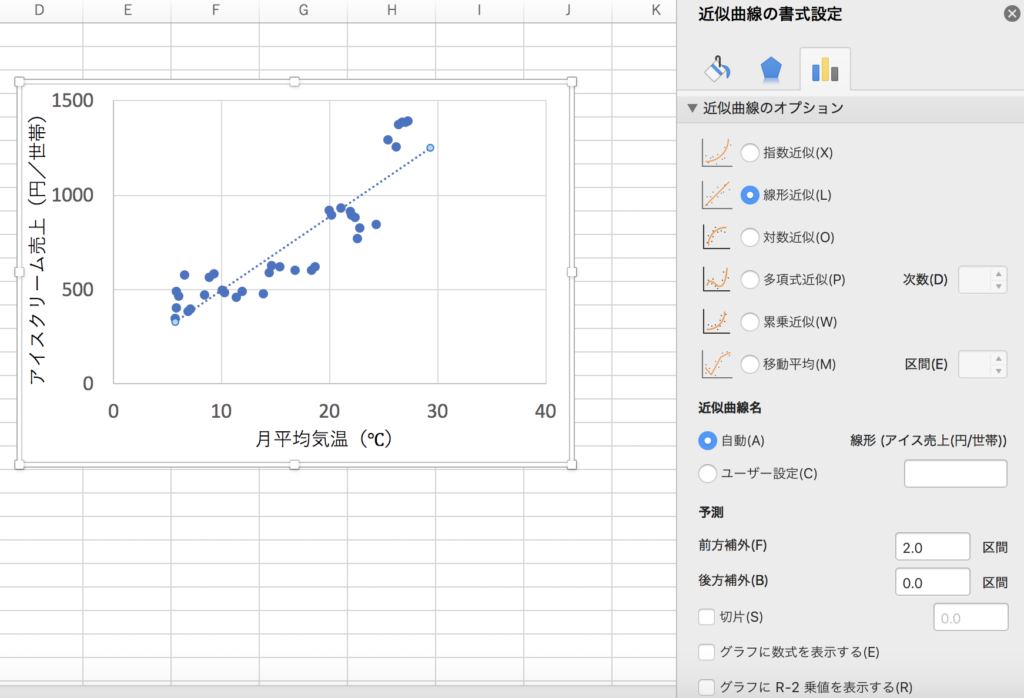

さて、上記の関数とグラフを先程のExcelに追加してみると、月別のアイスの売上は39.103×平均気温+106.73で予測できる、ということが分かりました。決定係数の0.808というのも、それなりに信頼できる数値でしょう。

この予測モデルを持っておくと、例えば来月の気温が20℃だと予測されているならば、アイスの売上は先程の数式を用いれば39.103×20+106.73=888.79円と予測できる・・・という訳です。

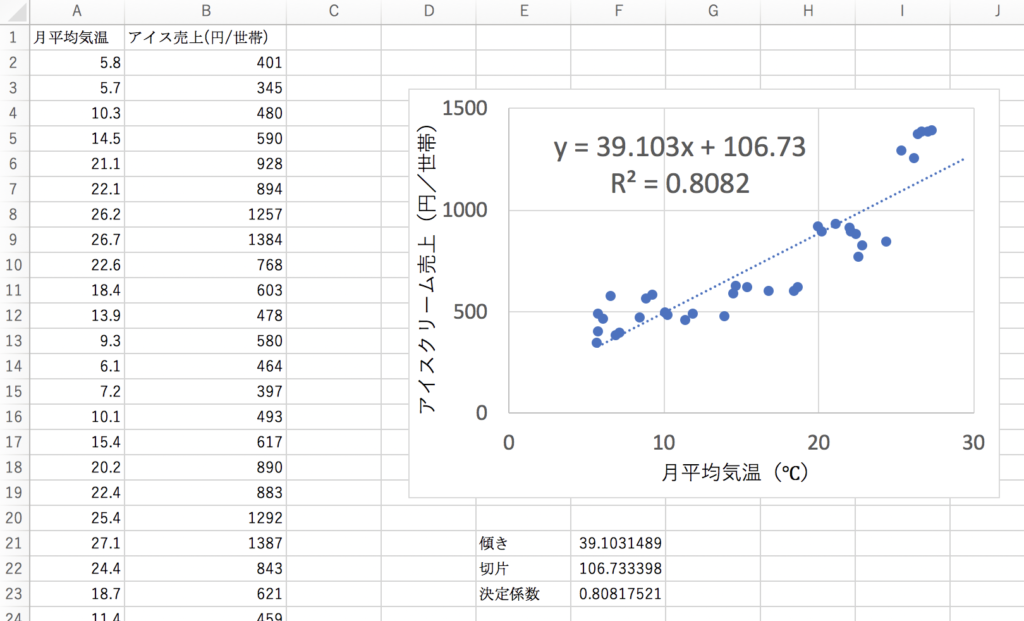
ただし、ひとつ注意点としては、このデータは気温5℃〜30℃あたりの情報しかありません。
つまり、気温5℃〜30℃ならばそれなりに予測に使えるでしょうが、0℃や35℃の時の予測の役に立つ保証はありませんので注意しましょう。

結果を信じる前に・・・

さて、回帰分析自体はこれで完了しているのですが、この結果だけを見て、「予測モデルができた！」と安心してはいけません。
このモデルがどれだけ信頼に値するものかを人間の目で確かめてあげましょう。

データ数は充分か？

まず、基本的にデータ数は多ければ多いほど良いです。
データが少ないと、たまたまデータが直線っぽく並んでいるだけの可能性が出てきてしまいますので。
極端な話、データ数が2つしか無ければ、必ずその2点を通る直線を引けますので、精度100%の予測モデルが出来てしまいます。
決定係数も1になります。・・・が、これでは意味がありません。
必ず幾つ以上ならばOKという決まりは無いのですが、一つの目安として30データ以上あることが望ましいでしょう。

外れ値は無いか?

「データ」というのは往々にして間違いがあったり、突飛な値が幾つか含まれてしまっているものです。
例えば、とある会社の社員に年収アンケートを取って、その「年齢」と「年収」のグラフを書いたときに以下のような結果になったとします。

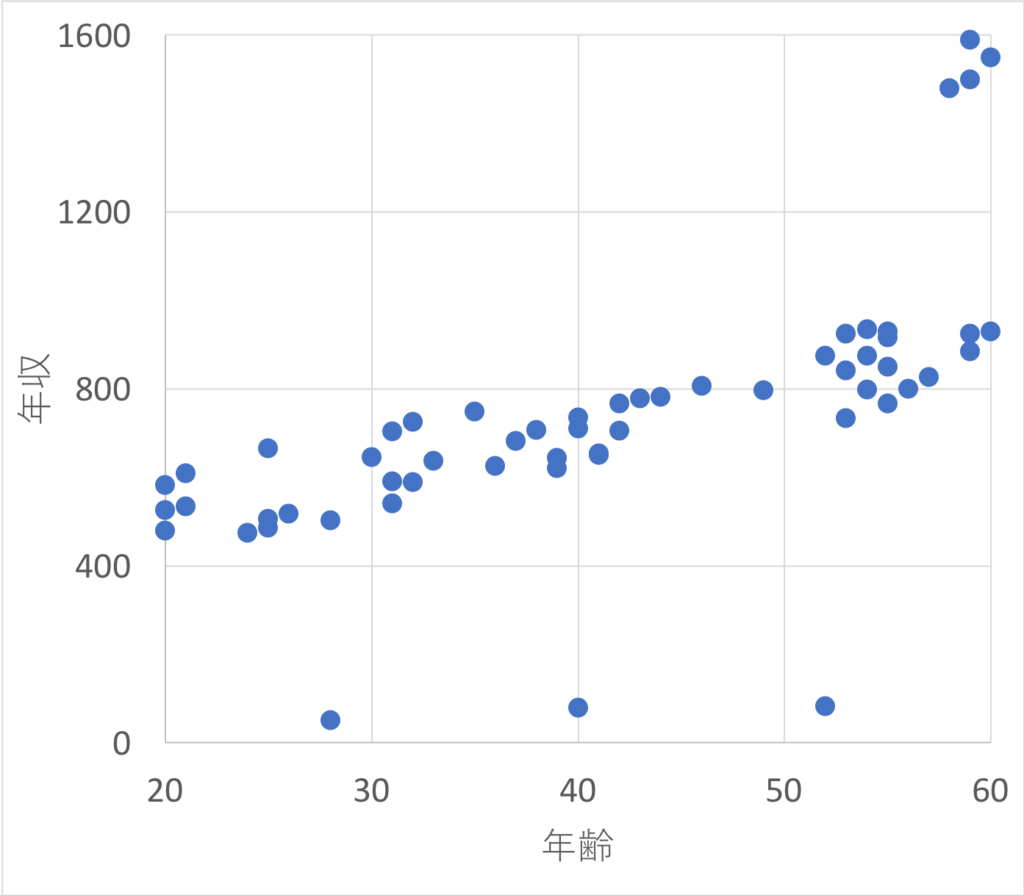
何やら、秩序を乱している値が幾つかあるように見受けられます。
これは、実は上に飛び出ている4点は会社役員のデータ。下に飛び出ている3点は、間違えて1/10の数値を入力してしまったデータです。

こういうデータを何も考えずに回帰分析してしまうと、正しい結果が得られなくなる可能性がありますので注意しましょう。

例えば、間違いのデータは値を修正するか、正解が分からないようならばいっそ除いてしまう。突飛な数値が含まれる場合は、「役員」と「その他の社員」で別に回帰分析を行う、など臨機応変に対応しましょう。

直線で良いのか？1変数で良いのか？

今回は、「直線」かつ「1変数」に絞って説明しましたが、冒頭にも述べたとおりデータの関係性は必ずしも直線関係とは限らず、そして重要な変数が複数存在する場合もあります。

曲線関係になる場合は、二次関数なのか、対数関数なのか、などどの曲線を選ぶかをきちんと考えることが必要です。

多変数になる場合は、まず重要になりそうな変数を洗えるだけ洗い出して、そこから不要そうな変数を切り捨ててゆけば良いでしょう。
アイスの例で言えば、「気温」だけでなく「湿度」「天気」「曜日」・・・など売上に関係しそうな変数をできるだけ持ってきてから、必要なさそうな変数を削ってゆくイメージです。
このような、2変数以上を用いて予測モデルを作る手法を重回帰分析と呼びます。・・・が、重回帰分析を行うためには、まずは普通の回帰分析を理解しなければいけません。