予測された「ランキング」がどれだけ正解に近いかを評価したい事があります。
例えば、Googleのような文章検索システム。
例えば「人工知能 仕組み」という言葉で検索したとすると、関連するホームページが上位に大量に出てきます。
人工知能の仕組みについて述べたページが5000ページあったとして、その全てが上位5000位に固まっていれば完璧です。
しかし、実際にそうなっているとは考えづらく、1000位くらいの順位になってくると、あまり関係無いページも徐々にランキングに現れるようになってきます。
このように、正解が複数あり、結果がランキングとなっている性質を持ったものの性能を測るにはどうすれば良いのでしょうか。
その方法もたくさんありますが、今回はその中でもシンプルな手法である「平均適合率」について説明します。
平均適合率(Average Precision)
単語だけ見てしまうと勘違いしてしまうのですが、「平均適合率」は全要素の「適合率」を単純に平均した値ではありませんのでご注意下さい。
ここで、ランキングの1位、4位、5位・・・に正解があったとしましょう。
ランキング1位までを見た時の適合率、ランキング4位までを見た時の適合率、ランキング5位までを見た時の適合率・・・を、すべて計算していきます。
この平均値こそが、「平均再現率(Average Precision)」です。

文章だと分かりづらいので、図にしてみます。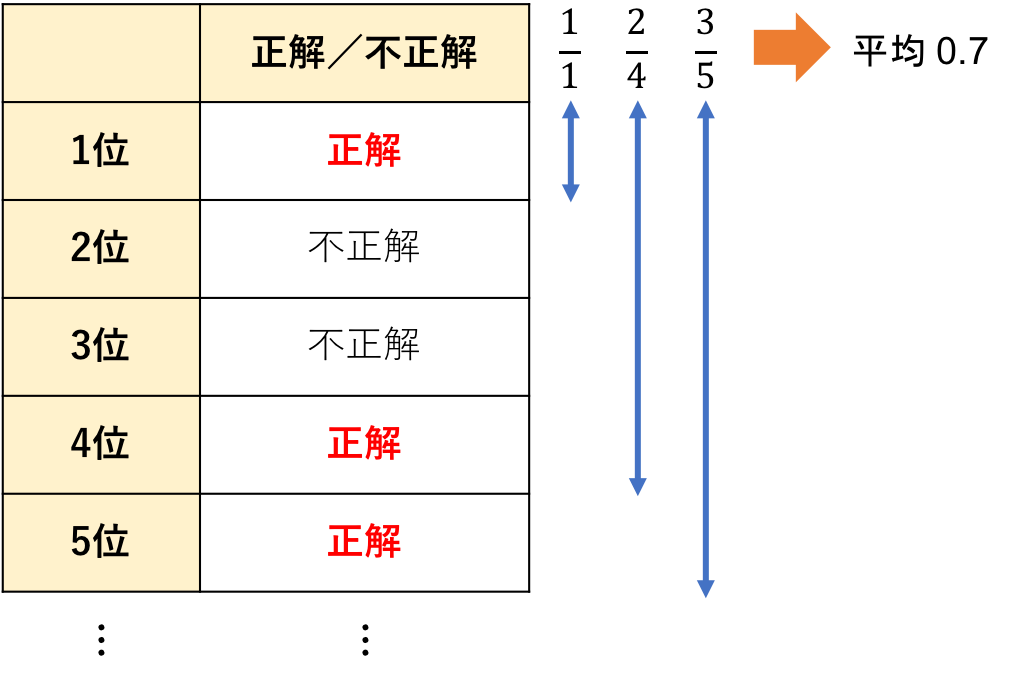
このレコメンドの精度は0.7だと計算されるようです。
仮に正解がすべてランキング上位に寄っていたら、\(\frac{1}{1}+\frac{2}{2}+\frac{3}{3}+\)…の平均値、という事で平均適合率は「1」となります。
Mean Average Precision
「Mean Average Precision」、通称MAPと呼ばれる指標についてです。
「Mean」も「Average」も和訳すると「平均」になってしまうので適切な和訳が難しいからか、日本でも一般的に「MAP」と呼ばれます。
これは、単に試験データ全てにおける「平均再現率」を平均したものです。
テストデータを2つ用意して、1つ目における平均再現率(AP)が0.7、2つ目における平均再現率が0.5ならば、MAPは0.6になります。
一般的にテストデータが1つである事は無いので、システムの性能指標としてはこちらのMAPを使うことになる場合が多いかと思います。
打ち切り
先程のGoogle検索の例のように、検索対象も正解も山ほどあると計算が大変です。
検索結果は何千万件も引っかかるかもしれませんが、検索順位10000位や20000位なんて殆どの人が見ません。
なので、平均適合率の計算も、ある程度の順位で打ち切っても問題なさそうです。
平均再現率の計算を100位までで打ち切る場合、「AP@100」というように表現します。
同様に「MAP@100」という表記もあります。
どこまでの順位を確認すべきかは時と場合によって変わります。
全体数が少なければ全部使っても良いですし、上位10件以外はどうでも良いならMAP@10を使うなど、臨機応変に使い分けてください。
おわりに
ランキングを考慮した性能指標はAP、MAP以外にも色々とあります。
しかし、シンプルな手法の中ではこれが最も多用される手法ではないでしょうか。
決して計算の理論が難しい手法ではないので、正しく理論を理解し、より効果的な性能指標を設定してください。