Pythonによる回帰分析と結果の可視化

Pythonを使って回帰分析を行ってみましょう。
理論や用語についてはこちらをご覧ください。

エクセルによる回帰分析

データの読み込み

まずは何はともあれ、データを読み込みます。
今回は「気温とアイスクリームの売上」データを読み込み、その関係性を調べてみます。
そして、それに基づいて翌日以降の予想気温からアイスクリームの売上を予測してみましょう。

ちなみに、ファイルは以下のような形式になっています。
– 既知のデータ(sales_data.csv)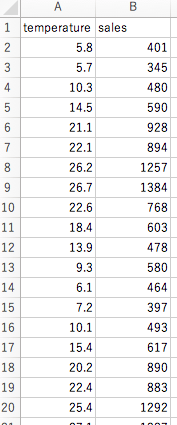

– 予測対象データ(sales_future.csv)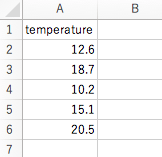

それでは、以下の通り2つのcsvを読み込みます。

続いてはsales_data.csvに基づいて回帰分析を行い、sales_future.csvに対して売上予測をしてみます。

回帰分析の実行

Pythonで回帰分析を実行するためのパッケージには幾つかあるのですが、個人的には回帰分析の実行結果が詳細に確認できる「statsmodels」をオススメします。
statsmodelsを使うと、以下のように回帰分析が簡単に実行できます。

まずは読み込んだcsvをxとyに分離します。
求めたいもの(目的変数)が「y」で、その計算に使うもの(説明変数)が「x」です。
これに関しては人間が指定してあげる必要があります。

ちなみに、「add_constant」は、切片を使う場合に指定します。つまり\(y=ax+b\)の\(b\)の項を使う場合には付けます。多くの場合は使うかなと。
そして、最後にresult.summary()をprintすると以下が表示されます。

何やら色々出てきました。
勿論すべて大事な指標なのですが、とりあえず\(a\)と\(b\)と\(R^2\)値は確認しておきましょう。
中段にある「coef」と「const」が交わった所にある数字が切片です。今回の例では106.7334です。
「coef」と「temperature」が交わったところにある数字が傾きです。今回の例では39.1031です。
そして、右上にある「R-squared」が\(R^2\)値になります。今回の例では0.808なので、そこそこ信用に値する結果になっていそうです。
いずれもExcelで実行した時と同じ結果が得られているようです。

結果として、アイスクリームの売上を\(y\)、気温を\(x\)とすると、\(y=106.7x+39.1\)という関係があるという答えが出ました。

未知のデータの推測

さて、回帰分析が出来た所で、お次は明日以降の予想気温をもとにアイスクリームの売上を予測してみます。
まあ、先程計算できた式の\(x\)に数値を入れて計算するだけではありますが・・・。

それでは冒頭で読み込んだdf_testを呼び出し、それと先程計算した\(a\)と\(b\)の値を用いて予測売上を計算してみましょう。

result.params.constには切片が、result.params[●]には●の傾きが格納されています。
上記のプログラムを実行すると・・・

df_testの上から順番に\(y\)が計算されました。
あとは以下のようにすれば、Excelに推測結果を書き出すことができます。

冒頭で読み込んだファイルに、\(y\)が追記されたresult.csvが出来ました。

回帰分析結果のグラフ化

折角なので、グラフも書いてみましょう。

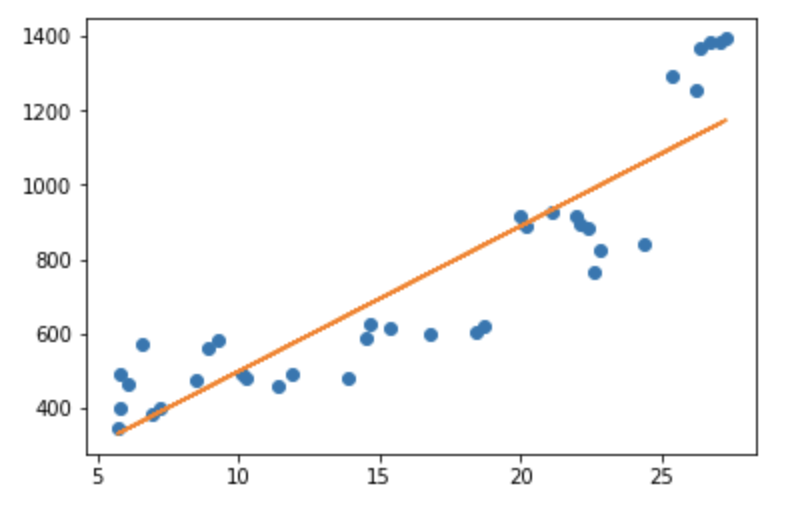
そこそこ良い回帰分析が出来ていそうですね。
単回帰分析であれば、何はともあれグラフを書いてみると、回帰分析の精度が直感的に分かりやすくなって良いと思います。

まとめ

さて、今回はPythonで回帰分析を行ってみました。
流れとしては、まず人間はデータを読み込ませて、\(x\)と\(y\)を指定してあげる。
そして回帰分析自体はコンピュータにやらせて、出てきた結果をどう解釈するかを人間が考える。
・・・おおよそこういった流れとなっています。

ちなみに重回帰分析も、xの列が増えるだけの話ですので、ほぼ同様の手続きで行うことができます。