Pythonで重回帰分析を行ってみます。
先にPythonによる単回帰分析の記事を読んでいただいたほうが分かりやすいかもしれませんが、こちらのみ読んでいただいても分かるようにはしております。
また、今回もstatsmodelsライブラリを使用します。

データの読み込み・重回帰分析の実行
今回は以下のようなデータを用いて、「temperature」(=気温)「price」(=アイスの値段)「rainy」(=雨かどうか)の3データから、「sales」(=アイスの売上)を予測してみます。
– 既知のデータ(sales_data.csv)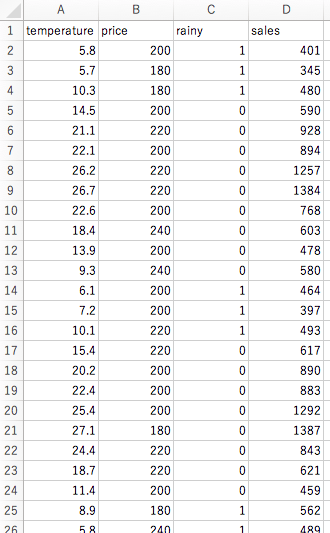
– 予測対象データ(sales_future.csv)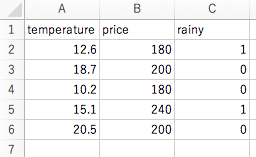
まずは以下のようにデータを読み込んで、回帰分析を実行します。
ここは単回帰分析とほとんど一緒です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
#CSV読み込み df = pd.read_csv("sales_data_j.csv") df_test = pd.read_csv("sales_future_j.csv") #目的変数名の指定 y_name = "sales" #従属変数(使用列)の選択 X_name = ["temperature", "price", "rainy"] #Xとyに分離 X = df[X_name] y = df[y_name] #回帰分析 import statsmodels.api as sm model = sm.OLS(y, sm.add_constant(X)) result = model.fit(disp=0) print(result.summary()) |
回帰分析に用いる列をX_nameに指定しています。
そして、最後のprintを実行すると・・・
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
OLS Regression Results ============================================================================== Dep. Variable: sales R-squared: 0.840 Model: OLS Adj. R-squared: 0.825 Method: Least Squares F-statistic: 55.83 Date: Sun, 07 Jul 2019 Prob (F-statistic): 8.19e-13 Time: 17:07:05 Log-Likelihood: -225.71 No. Observations: 36 AIC: 459.4 Df Residuals: 32 BIC: 465.8 Df Model: 3 Covariance Type: nonrobust =============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------- const -340.9653 303.596 -1.123 0.270 -959.371 277.440 temperature 48.2076 4.818 10.005 0.000 38.393 58.022 price 1.1667 1.314 0.888 0.381 -1.511 3.844 rainy 193.0358 77.940 2.477 0.019 34.277 351.794 ============================================================================== Omnibus: 1.521 Durbin-Watson: 1.822 Prob(Omnibus): 0.467 Jarque-Bera (JB): 1.072 Skew: -0.112 Prob(JB): 0.585 Kurtosis: 2.185 Cond. No. 2.82e+03 ============================================================================== |
「月平均気温」の値を\(x_1\)、「値段」の値を\(x_2\)、「雨」の値を\(x_3\)、とすると、\(y=48.2 x_1+1.2 x_2+193.0 x_3-341.0\)という関係があるという関係が分かりました。
上部の「Adj. R-squared」が「自由度調整済み\(R^2\)値」に当たり、0.825と計算されています。
中段の表内の「P>|t|」が、変数ごとのp値を表します。
いずれもExcelによる重回帰分析と同じ結果のようです。
変数の選択
重回帰分析で大切なのは、どの変数が大事で、どの変数が不要なのかをきちんと見極める事です。
例えば、上の結果を見てみると、「price」のp値が低いので、「price」列を消して重回帰分析してみたいですね。
その時、Excelだと、自ら不要な列を消して、再度、「データ分析」メニューから使用列を選択して重回帰分析を実行・・・という手順を踏まなければいけません。
しかしpythonでは「使う列の名前」を変更してプログラムを実行してあげるだけです。
今回の例で言えば、上記プログラムのX_nameをX_name = ["temperature", "price", "rainy"]
からX_name = ["temperature", "rainy"]
と変更し、実行するだけでOKです。
すると、以下のようになりました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
OLS Regression Results ============================================================================== Dep. Variable: sales R-squared: 0.836 Model: OLS Adj. R-squared: 0.826 Method: Least Squares F-statistic: 83.88 Date: Tue, 09 Jul 2019 Prob (F-statistic): 1.15e-13 Time: 10:18:19 Log-Likelihood: -226.15 No. Observations: 36 AIC: 458.3 Df Residuals: 33 BIC: 463.0 Df Model: 2 Covariance Type: nonrobust =============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------- const -86.2107 98.682 -0.874 0.389 -286.980 114.559 temperature 47.6485 4.762 10.007 0.000 37.961 57.336 rainy 178.0815 75.852 2.348 0.025 23.759 332.404 ============================================================================== Omnibus: 3.161 Durbin-Watson: 1.821 Prob(Omnibus): 0.206 Jarque-Bera (JB): 1.483 Skew: 0.031 Prob(JB): 0.476 Kurtosis: 2.008 Cond. No. 94.6 ============================================================================== |
こちらも、Excelの時と同様の結果が得られているようです。
「Adj. R-squared」が先程より僅かに上がり、「temperature」と「rainy」のp値も低いことから、「price」を用いないほうが良い推測だと考えられます。
未知のデータの推測
それでは、「temperature」と「rainy」を用いて、未知のデータに対する予測をしてみます。
といっても先の回帰分析の結果と、読み込んだ「sales_future_j.csv」を使って機械的に計算するだけになります。
ソースは以下。
|
1 2 3 4 5 6 7 8 9 10 |
y_result=[] #未知データの推測(重回帰) for i in range(len(df_test.index)): y_tmp = result.params.const for j in range(len(X_name)): x_name = X_name[j] y_tmp += result.params[x_name] * df_test[x_name][i] y_result.append(y_tmp) print(y_result) |
|
1 |
[692.242462219598, 804.8170009756097, 399.80442653785354, 811.3638076424675, 890.5843696800758] |
最後の「y_result」に結果が格納されました。
また、この結果をExcelに書き出したいのなら以下のようにします。(単回帰の時と一緒です。)
|
1 2 3 4 |
#結果書き出し df_test_y = pd.DataFrame(y_result,columns=["y"]) df_result = pd.concat([df_test,df_test_y],axis=1) df_result.to_csv("result.csv",index=None) |
作成されたresult.csvを見てみると・・・。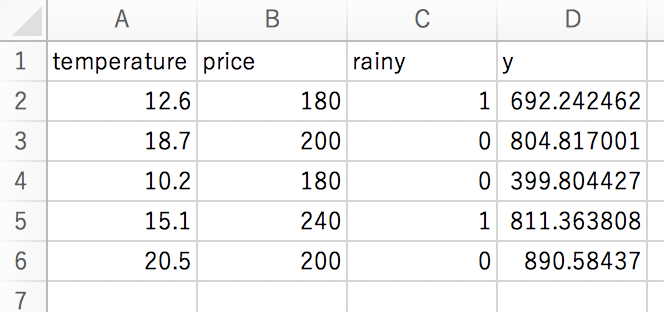
無事に先程の結果がcsvに反映されているようです。
まとめ
さて、今回はPythonで重回帰分析を行ってみました。
重回帰分析は今回扱った変数選択以外にも、データの欠損値や外れ値を除外したり、また「ほとんど同じ列」が含まれていないか確認したりと考えることはたくさんあります。
そう考えると、Excelでも計算は可能ですが、圧倒的にPythonの方が便利で自由度の高い分析ができます。
入力するcsvの形式を合わせれば、あとはソースのコピペで動くと思われますので、ご活用ください。