例えば、スマホアプリを作ってリリースはしたものの、一体、どんなユーザが登録してくれるのか。
性別、年齢・・・など、一体どんな傾向を持った人がユーザ登録してくれる傾向にあるのか。
それが分かれば様々なマーケティングの手が打てます。
そんな課題を解決してくれるデータ分析手法が「ロジスティック回帰分析」です。
本記事ではロジスティック回帰分析の理論を簡単に紹介した後、Pythonで実際にロジスティック回帰分析を実行する所までやってみます。
簡単に理論紹介
ロジスティック回帰分析は(重)回帰分析を応用した手法のひとつです。

回帰分析や重回帰分析で分かるのは基本的に「直線の関係」だけでした。
つまり、\(y=a_1 x_1+a_2 x_2+a_3 x_3+…+a_n x_n+b\)・・・という1次関数の関係です。
xを動かせば、yはどんな値も取ることができます。
しかし、今知りたいのは、「ユーザ登録する可能性は何%なのか」です。よって、xは幾つでもyは0〜1に収まっていて欲しいですね。
そこで、ロジスティック回帰分析では、上記の1次関数の式を下記のように少しいじります。
\[y=\frac{1}{1+e^{-(a_1 x_1+a_2 x_2+a_3 x_3+…+a_n x_n+b)}}\]
これがロジスティック回帰分析で用いる関数です。この式はxにどんな値が入ってもyは0〜1の値を取ります。
ロジスティック回帰分析は単に「この式を使って回帰分析する」というだけで、ほぼ通常の回帰分析と一緒です。
Pythonでロジスティック回帰分析を行う
では、今回は以下のようなデータ(user_data.csv)を用いてロジスティック回帰分析を行ってみます。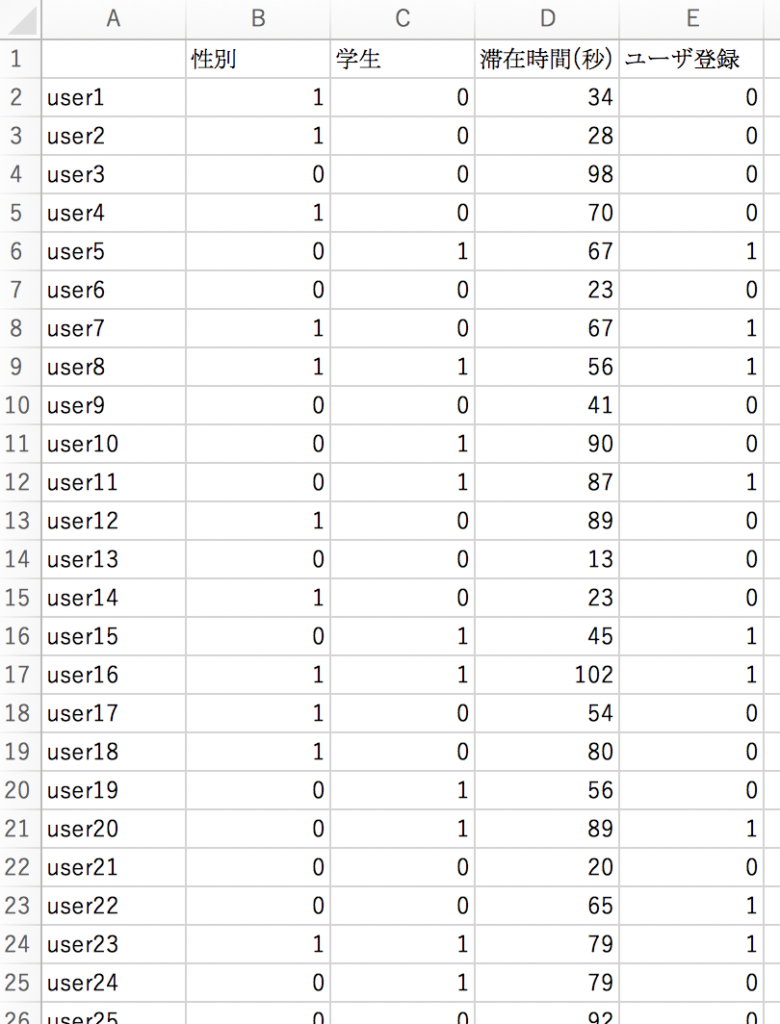
このように要因データには、「性別」のようなカテゴリー情報だけでなく、「滞在時間」のような数値情報も含めることができます。
このデータを用いて早速ロジスティック回帰分析を行っていくのですが、statmodelsパッケージを使えば通常の回帰分析とほぼ同様の書き方で実行できるので、一気に行きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import numpy as np import pandas as pd #CSV読み込み df = pd.read_csv("user_data.csv") #目的変数名の指定 y_name = "ユーザ登録" #従属変数(使用列)の選択 X_name = ["性別", "学生","滞在時間(秒)"] #Xとyに分離 X = df[X_name] y = df[y_name] #ロジスティック回帰分析 from sklearn.linear_model import LogisticRegression import statsmodels.api as sm model = sm.Logit(y, sm.add_constant(X)) result = model.fit(disp=0) print(result.summary()) |
上記を実行すると・・・
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Logit Regression Results ============================================================================== Dep. Variable: ユーザ登録 No. Observations: 40 Model: Logit Df Residuals: 36 Method: MLE Df Model: 3 Date: Thu, 25 Jul 2019 Pseudo R-squ.: 0.2588 Time: 03:58:19 Log-Likelihood: -19.615 converged: True LL-Null: -26.463 LLR p-value: 0.003350 ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ const -4.2982 1.555 -2.764 0.006 -7.346 -1.250 性別 0.5251 0.842 0.624 0.533 -1.124 2.174 学生 2.0147 0.841 2.396 0.017 0.367 3.663 滞在時間(秒) 0.0390 0.019 2.087 0.037 0.002 0.076 ============================================================================== |
※表の見方等については重回帰分析のページにて。
ちなみに、直線関係の回帰分析以外には一般的にR2値は計算されません。
ロジスティック回帰分析の場合は、その代用である「Pseudo R-squ.」を見るか、p値から精度を判断していくことになります。
ここでp値を見てみると、ユーザ登録してくれるかどうかには、「学生かどうか」と「滞在時間の長さ」が重要なようです。
逆に、性別は殆ど関係なさそうです。ということで、性別は抜いてもう一回実行してみます。
X_name = ["性別", "学生","滞在時間(秒)"]
を、X_name = ["学生","滞在時間(秒)"]
にするだけでOKです。
すると・・・。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Logit Regression Results ============================================================================== Dep. Variable: ユーザ登録 No. Observations: 40 Model: Logit Df Residuals: 37 Method: MLE Df Model: 2 Date: Sat, 27 Jul 2019 Pseudo R-squ.: 0.2513 Time: 14:44:11 Log-Likelihood: -19.813 converged: True LL-Null: -26.463 LLR p-value: 0.001295 ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ const -4.1094 1.507 -2.728 0.006 -7.062 -1.157 学生 1.8831 0.798 2.361 0.018 0.320 3.447 滞在時間(秒) 0.0403 0.018 2.188 0.029 0.004 0.076 ============================================================================== |
すべてのp値が低くなり、良い推定になっていそうですね。
これより、を「ユーザ登録する可能性」を\(y\)、「学生かどうか」を\(x_1\)、「滞在時間(秒)」を\(x_2\)とすると、
\[y=\frac{1}{1+e^{-(1.8831 x_1+0.0403 x_2-4.1094)}}\]
と予測できることが分かりました。
未知データの推測
どのユーザ登録してくれる人の傾向は分かりましたが、お次は未知データの予測もやってみます。
つまり、「学生かどうか」「滞在時間」の2つの情報から、その人がユーザ登録してくれる確率を求めることになります。
予測に使うデータ(user_data_future.csv)は以下。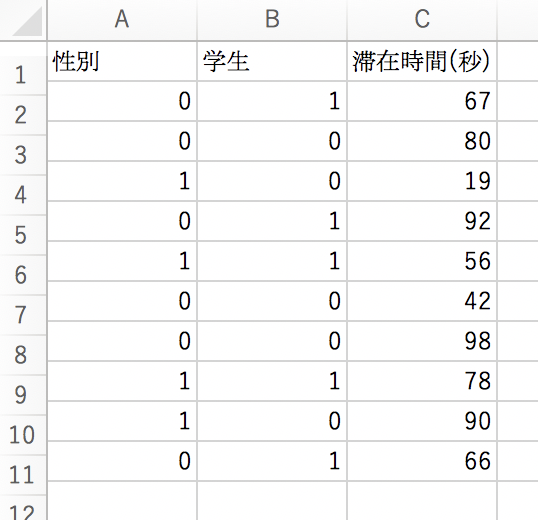
こちらも、ほぼ通常の重回帰分析と同様のやり方となりますが、先に述べたとおり回帰分析に使う式が違うのでちょっとだけ計算式も変わります。
|
1 2 3 4 5 6 7 8 9 10 11 |
###未知データの推測 df_test = pd.read_csv("user_data_future.csv") import math y_result=[] for i in range(len(df_test.index)): y_tmp = result.params.const for j in range(len(X_name)): x_name = X_name[j] y_tmp += result.params[x_name] * df_test[x_name][i] y_result.append(1 / (1 + math.e**-y_tmp)) print(y_result) |
最後にeの計算が入るので、mathパッケージを呼び出しています。
上記を実行すると・・。
|
1 |
[0.6170412161588048, 0.2928466124681998, 0.03413222194098345, 0.8154306982851297, 0.5082962248385622, 0.08205130708481542, 0.4612411916120478, 0.7152109821321985, 0.38269487197510876, 0.6074631589429199] |
予測したい10個のデータについて、上から順番に「ユーザ登録する確率」が計算されています。
するorしないをはっきりさせたい場合は、「0.5以上ならユーザ登録する、0.5未満ならしない」と考えて良いでしょう。
この結果をExcelに書き出したい場合は通常の回帰分析と同様なのでそちらをご覧ください。
まとめ
以上がPythonを利用したロジスティック回帰分析の方法でした。
といっても、ほぼ回帰分析と一緒で、ただ推測に用いる数式が異なるというだけの話です。
「求めたい結果が数量ならば回帰分析、確率ならばロジスティック回帰分析」と両者を使い分けてください。