2015年あたりから、「AIと言えばディープラーニング(深層学習)」というくらい、ディープラーニングの実力やその可能性・発展性が浸透してきたように感じます。
確かに画像認識を行いたいのなら今やディープラーニング一択に近いですし、音声認識や自然言語処理にもディープラーニングの実力は遺憾なく発揮されています。
ここまで影響が広まったのは、研究者の方々の素晴らしい研究が礎にあるのは勿論のこと、今や開発用の便利なパッケージ、ライブラリが無償公開されており、誰でもディープラーニングを簡単に扱えることになったことが大きいでしょう。
・・・が、それは裏を返せば「ディープラーニングの理論を知らなくてもディープラーニングの開発ができる」という状況にもなってしまった、ということでもあります。
しかも、結構、見よう見まねで適当に作ったAIが良い結果を弾き出したりします。
よって、ディープラーニングの事を殆ど知らないでディープラーニングの開発やチューニングを行う「AIエンジニアもどき」も多くなってしまったわけです。
ディープラーニングがどのような物で、どのような手続きを経て「学習」しているのか。
そのアウトラインを知っておくと、闇雲でない学習パラメータ調整や、闇雲でないデータクレンジングの検討が出来るようになり、「とりあえず作れる」AIエンジニアもどきとは差別化が図れます。
ディープラーニングの手法も色々ありますが、基本は一緒です。本記事はディープラーニングの基本の仕組みをご説明します。
ディープラーニングとは
ディープラーニングというのは「機械学習」の手法のうちの1つです。
機械学習というのは人間が行うような「学習」をコンピュータに行わせる技術です。
その中でも、ディープラーニングは「ニューラルネットワーク」と呼ばれる機構を用いる機械学習の手法となります。
ニューラルネットワークについては次項で。
ニューラルネットワークとは
ニューラルネットワークとは、言わば「仮想の脳みそ」のようなものです。
人間の脳の構造を模して作られた、”自分でモノを考える機構”という感じでしょうか。
そして、ニューラルネットワークは「形式ニューロン」という物質が幾つも集まった構造をしています。
形式ニューロンとは
形式ニューロンと言うのは、「複数の数値を受け取って、1つの出力を返す関数」です。
生物の脳が持っている「ニューロン」を模式しています。
形式ニューロンは、受け取った数値それぞれに対して重み付けをすることができます。
これにより、どの入力が大事で、どれが大事じゃないかを適切に切り替えることができます。
もう1つ、自分自身で、入力された数値に幾らか足したり引いたりして、入力値を調節することもできます。
これを「バイアス」と呼びます。
図にすると以下のようなイメージです。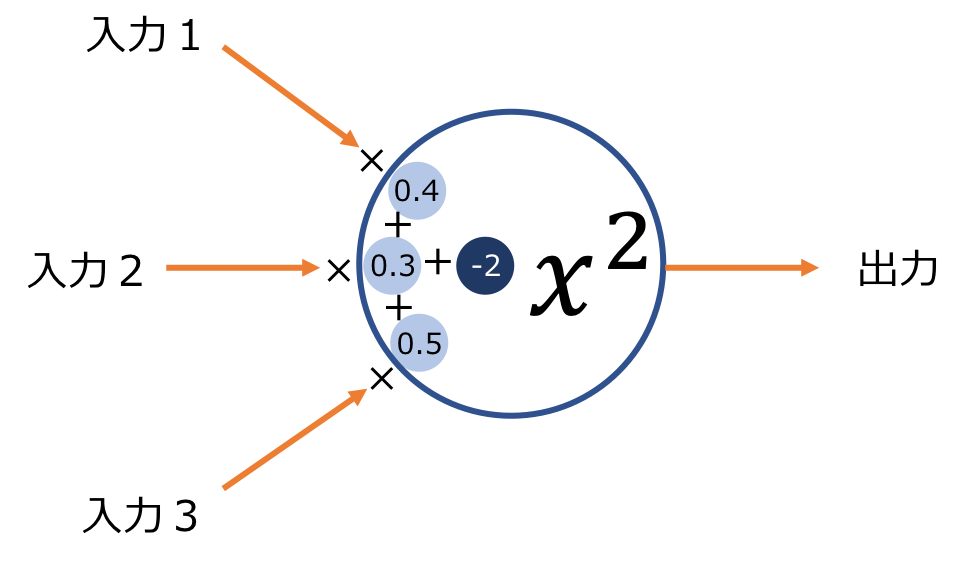
上の例では、例えば入力に2,4,6を入力すると、
2 × 0.4 + 4 × 0.3 + 6 × 0.5 – 2 = 3
なので、それを二乗した「9」が最終的な出力となります。
この関数は生まれつきのもので、変えることは出来ません。
上記のように、「2乗する形式ニューロン」として生まれたら、それはそのままです。
しかし、「重み」「バイアス」は状況によって変化させることができます。
正確な定義だと「形式ニューロン」の出力は0か1の二値のみですが、ニューラルネットワークに用いる「形式ニューロン」の出力は一般的に任意の数値を取ります。
また、用いられる形式ニューロンの関数も「Sigmoid関数」「ReLU関数」「Softmax関数」など色々あり、この関数のことを「活性化関数」と呼びます。
ディープラーニングの実行
ニューラルネットワークの選択
さて、先に述べたとおり、「形式ニューロン」が複数組み合わされたものがニューラルネットワークです。
ディープラーニングを行うには、まずニューラルネットワークを用意する必要があります。
今回は仮に以下のような課題を考えてみます。
あるコインの「直径」と「重さ」情報から、そのコインが「レア物」か、「普通」か、「偽物」かを判別させるニューラルネットワークを作成する
さて、この課題をディープラーニングで解決してみましょう。
ここで、「どの関数の形式ニューロンを、どのように組み合わせたニューラルネットワークにするか」を決めるのは人間の仕事です。
いちいち考えるのは面倒・・・というよりもどの構造が適しているかなんて基本的には分かりません。
なので、一般公開されているニューラルネットワークを拝借する場合が多いです。
「VGG」「AlexNet」「GoogLeNet」など、公開されているニューラルネットワークにも色々あります。
どれが絶対に良いという決まりはありませんが、「画像認識に強い」「音声認識に強い」など、それぞれの特徴はありますので、自分が行いたいタスクに見合ったニューラルネットワークがどれなのかを調べて適用するのが良いでしょう。
ただ、上記のニューラルネットワークはわりと複雑で解説にはあまり向かないので、今回は一例として以下の単純なニューラルネットワークを考えてみます。形式ニューロンの活性化関数は、中間層は「ReLU関数」、出力層は「Softmax関数」にしてみます。
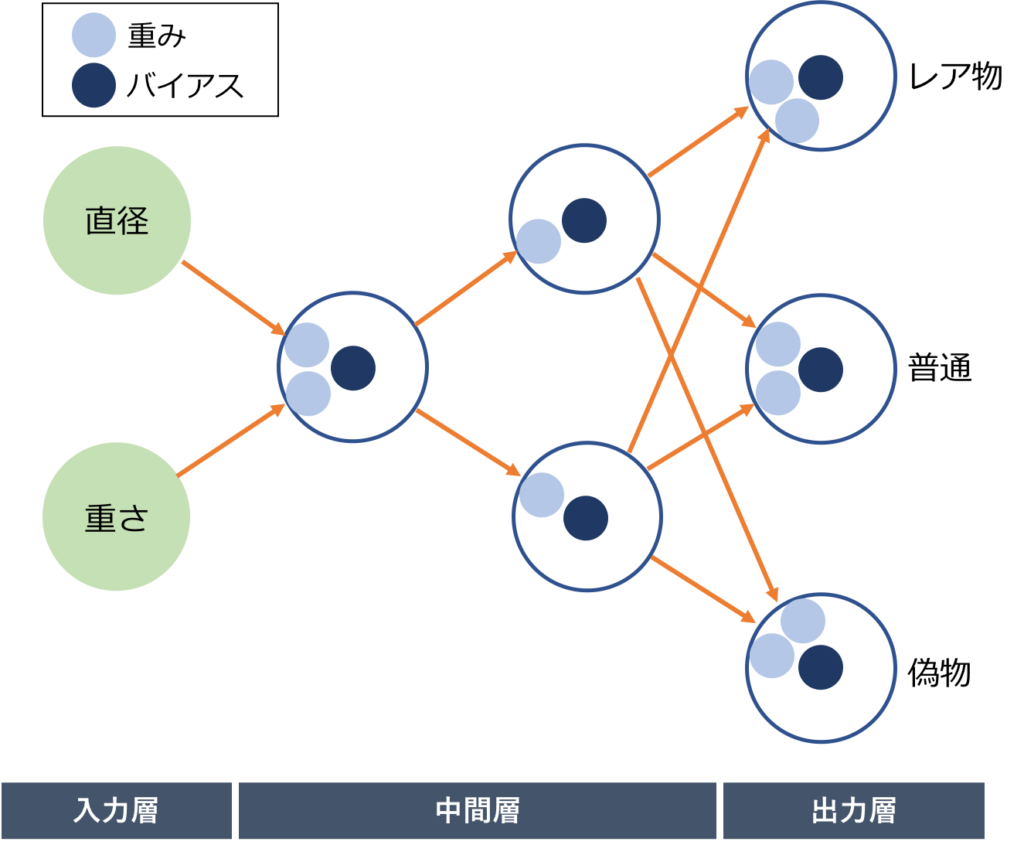
ニューラルネットワークを構成する際に、各形式ニューロンの活性化関数を何にするか決める必要があります。
一概に何を使うと良いとは言えないのですが、中間層には「ReLU関数」が良く用いられます。
出力層は「Softmax関数」を用いることが一般的です。(今回のような「分類タスク」の場合に限ります)
「どんな構造が適しているか分からない」と言っても、入力の個数と、出力の個数は決まっています。
今回の例では、判別するためには「直径」と「重さ」の2値が必要なので、「入力」は2つ用意しておきます。
出力は「レア物」or「普通」or「偽物」の3パターンが必要なので、「出力」は3つ用意しておきます。
そうすれば、入力された「直径」「重さ」を持つコインが「レア物」の場合は、3つの形式ニューロンの出力が「1/0/0」となるように。
「普通」の場合は、3つの形式ニューロンの出力が「0/1/0」となるように。
「偽物」の場合は、3つの形式ニューロンの出力が「0/0/1」となるように。
・・・そのようになる、各形式ニューロンの「重み」「バイアス」を考えていくだけです。
が、重みとバイアスの適切な値なんて、どうすれば分かるのでしょうか。
実はこの適切な「重み」「バイアス」の値を調べていく作業がこそ、ニューラルネットワークの「学習」と呼ばれる部分です。
初期の重み・バイアスの決定
さて、「重み」「バイアス」を適切な値にしたいとは言っても、初めは適切な値なんて分かりません。
それは人間もコンピュータも同じです。
色々と実験していくことによって、徐々に適切な値が見えてきます。
「事前学習」と呼ばれる手法を使うと、「重み」「バイアス」の初期値をどの程度にしておいたら良いかの目星が付けられます。
一般的にはこの事前学習により初期値を決定しますが、その理論については本記事では省略致します。
教師データを与える
さて、ここで「教師データ」の出番です。
教師データと言うのは、「入力と出力の正解ペア」です。
上の例では、
レア物:「直径15.1mm、重さ9.1g」「直径15.3mm、重さ9.2g」
普通:「直径15.3mm、重さ8.9g」「直径15.2mm、重さ9.0g」
偽物:「直径15.0mm、重さ9.0g」「直径15.2mm、重さ9.1g」
・・・などというデータになります。
つまり、上のニューラルネットワークにおいて、
・15.1/9.1を入力したら1/0/0が出力される
・15.3/9.2を入力したら1/0/0が出力される
・15.3/8.9を入力したら0/1/0が出力される
・15.2/9.0を入力したら0/1/0が出力される
・15.0/9.0を入力したら0/0/1が出力される
・15.2/9.1を入力したら0/0/1が出力される
・・・という状況が極力満たされるような「重み」「バイアス」の値を探る作業が、ディープラーニングにおける「学習」であると言えます。
ちなみに今回は説明の都合上、正解データを6個としていますが、実際はこれでは少なすぎるので最低でも1,000データくらいは欲しい所です。
順伝播
さて、正解データを準備したら、その入力値をニューラルネットワークに突っ込みます。
「重み」「バイアス」はもう決まっていますから、ここは計算していくだけです。
今回は以下のような「重み」「バイアス」を用いて、上の例の1個目の値(直径15.1mm、重さ9.1g)を入力してみます。
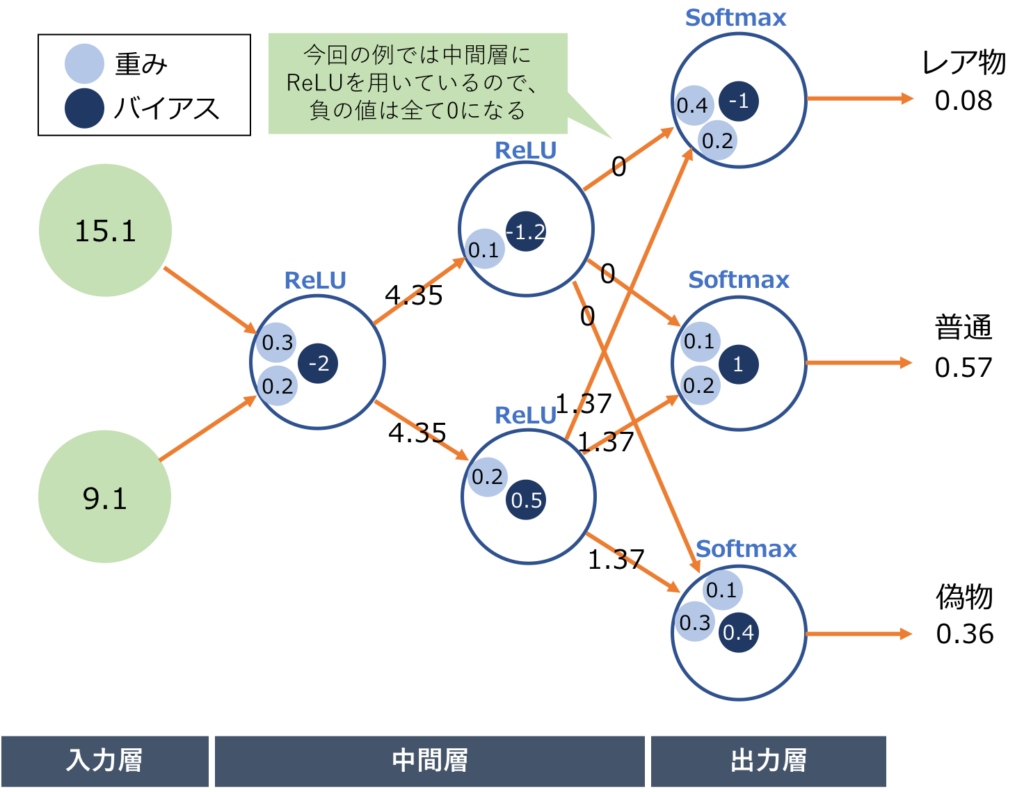
出力は上から「0.08/0.57/0.36」となりました。
しかし、この出力は期待している出力とは違います。本当は「1/0/0」になって欲しい訳です。
つまり「誤差」があるわけですね。
このような計算を6データ全てで実験し、最後にその誤差の大きさを足し算します。
それこそが、この「重み」「バイアス」の「誤差の大きさ」・・・すなわち、「精度」ということになります。
実際にディープラーニングを行うにあたり6パターンでは少なすぎ、例えば10,000個といったデータを扱うことになると先に述べました。
そうすると、たった1通りのバイアス・重みの精度(正解との誤差)を計算するのに10,000回も実験が必要になります。
それでは時間がかかって仕方ないので、正解データの一部を抽出して誤差の計算をする場合が一般的です。
これは「ミニバッチ」と呼ばれる手法です。
逆伝播
今度は「誤差」の計算結果を全ての形式ニューロンに伝えていきます。
ここで、誤差逆伝播法と呼ばれる手法を用います。
詳しい方法は割愛しますが、最終的な「誤差」と、順伝播の際に計算した各形式ニューロンの「入力値」「出力値」の情報を元にすると、
全ての「重み」「バイアス」に対して、重み(orバイアス)をx軸、誤差をy軸とした時のグラフの、現在の「重み(orバイアス)の値」における傾きを計算することができます。
図にすると以下のようになります。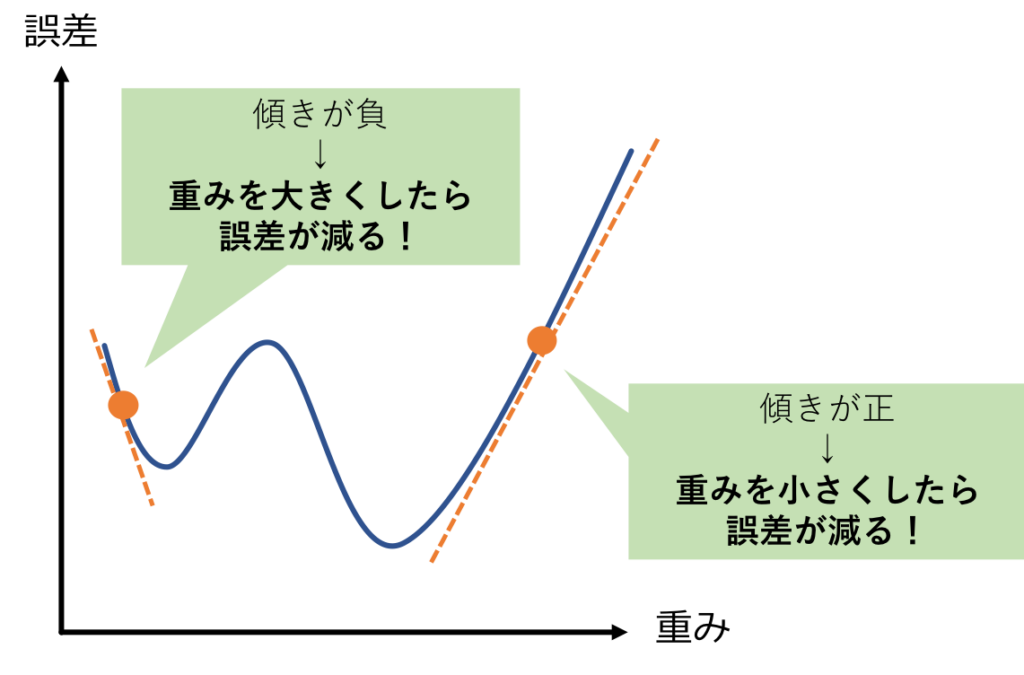
ある重みの傾きが「-10」ならば、「誤差を小さくするためには、自分の重みを増やせばいいのかな?」と考え、
傾きが「+3」ならば、「誤差を小さくするためには、自分の重みをちょっと減らせばいいのかな?」という風に考えます。
このように、出力層から命令を出され、全ての「重み」「バイアス」はそれに従って自身の値を調整します。
逆誤差伝播法では、各々の「重み」「バイアス」の傾きの大きさしかわかりません。
つまり、具体的に幾つくらい値を調整すべきかまでは分かりません。
その「どれほど調整するか」の値を学習率と呼び、その大きさは人間が指示します。
ただし、この調整の仕方のアルゴリズムも「ADAM」「RMSprop」「SGD」など色々と発表されていますので、ひとまずはそれらを適用してみるのが良いかと思います。
あとは順伝播・逆伝播・更新をひたすら繰り返す
さて、逆誤差伝播法を用いたことによって、全ての「重み」「バイアス」の値が調整されました。
ここまでで学習1回の完了となります。
続いては、この調整された「重み」「バイアス」の値を使ってふたたび順伝播を行い、逆伝播で「バイアス」「重み」を更新します。
この作業を何度も何度も繰り返すと、段々と「重み」「バイアス」が適切な値に近づいていきます。
学習を何回行うかは人間が決めるところですが、学習を繰り返していって、「もうこれ以上学習してもあまり変わらない(「重み」「バイアス」の値がほとんど変わらなくなってきた)」と思われるだけ学習したらストップすれば良いでしょう。
まとめ
さて、以上のディープラーニングの学習の流れをまとめると以下のようになります。
・ニューラルネットワークを構成する(構成、活性化関数、初期重み、初期バイアスなどを設定する)
・正解データをニューラルネットワークに入力し、その出力と「期待する出力」との誤差を計算する(順伝播)
・順伝播により求めた誤差と、各形式ニューロンの入出力情報から、「重み」「バイアス」を更新する(逆伝播)
・更新された「重み」「バイアス」の値でふたたび順伝播⇒逆伝播・・・を何度も繰り返す
このようにしてディープラーニングは学習を行います。
もちろん、全く使い物にならない学習モデルが出来ることもあるでしょうが、どんなタスクに対してもディープラーニングは最適な学習モデルを作ろうと努力してくれます。
人間はディープラーニングの特性を理解し、その学習ができるだけうまく進むように、正解データの準備やニューラルネットワークの構成、様々なパラメータの調整を行って、ディープラーニングの補助をしてあげることが大切です。