Pythonでデータを読み込み、列ごとに平均値や中央値などの「データの代表値」を計算してみましょう。
データ分析の初めの一歩は、何はともあれ平均値、中央値などの「代表値」を求めることです。
Excelでも計算は可能ですが、ファイルサイズが巨大な場合や、後々にもっと複雑な計算をしたくなってきた場合などはExcelでは手に負えません。
そこまで難しくない上に、慣れればExcelよりも簡素で高速に計算できますので、是非多くの学生や社会人の皆様に覚えて頂ればなと思います。
データの読み込み
まずは集計したいcsvを準備します。
今回は、以下のような「都道府県別の17歳時点における身長・体重データ」を実験データとして読み込んでみましょう。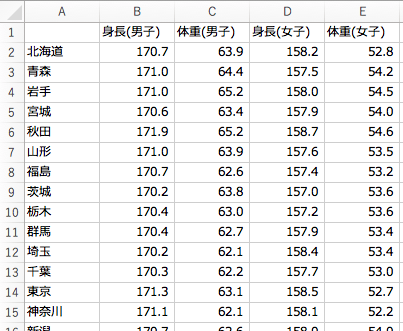
※参照元:e-Stat「学校保健統計調査」
何はともあれ、まずはPythonにデータを読み込ませます。
|
1 2 |
import pandas as pd df = pd.read_csv("data.csv",index_col=0) |
「index_col=0」というのは、「すでに行名(今回の場合は県名)は付いてますので、行名は付けないで良いですよ」という意味の引数です。
この時、文字コードがおかしいと正しく読み込まれない場合がありますので、ご注意ください。
もしこの時点でエラーが出たら、csvの文字コードを「utf-8」に変えておくのが一番てっとり早いかなと思います。
色々な代表値を一気に求める
さて、それではデータの代表値を色々と求めてみましょう。
実は、pythonのnumpyパッケージには、「decsribe」というデータの平均値、中央値などを一気に求められる便利関数が用意されています。
早速適用してみましょう。
|
1 |
print(df.describe()) |
実行してみると。。。
|
1 2 3 4 5 6 7 8 9 |
身長(男子) 体重(男子) 身長(女子) 体重(女子) count 47.000000 47.000000 47.000000 47.000000 mean 170.514894 62.885106 157.574468 53.127660 std 0.586062 0.999560 0.588465 0.611378 min 168.700000 60.800000 155.900000 51.700000 25% 170.300000 62.150000 157.250000 52.900000 50% 170.400000 62.800000 157.600000 53.100000 75% 170.900000 63.600000 158.000000 53.450000 max 172.100000 65.200000 158.700000 54.600000 |
一気に色々出てきましたね。
上から、「データ数」「平均」「標準偏差」「最小値」「第1四分位数」「中央値」「第3四分位」「最大値」となります。
有効数字が多すぎて見づらい場合は、以下のようにお尻に「.round(有効桁数)」を付けると、有効数字の桁数を変えられます。
例えば小数点以下2桁にしたければ、
|
1 |
print(df.describe().round(2)) |
とすれば、
|
1 2 3 4 5 6 7 8 9 |
身長(男子) 体重(男子) 身長(女子) 体重(女子) count 47.00 47.00 47.00 47.00 mean 170.51 62.89 157.57 53.13 std 0.59 1.00 0.59 0.61 min 168.70 60.80 155.90 51.70 25% 170.30 62.15 157.25 52.90 50% 170.40 62.80 157.60 53.10 75% 170.90 63.60 158.00 53.45 max 172.10 65.20 158.70 54.60 |
これで見やすくなりましたね。
知りたい所だけ求める
「そんな全部いらないから、知りたいやつだけ知りたい」という場合もあります。
また、describeの中にはない代表値(合計値、最頻値など)を求めたい場合もあります。
そういう場合のために、代表値別に個別のメソッドが用意されています。
例えば、「平均値」だけ欲しい場合は以下。
|
1 |
print(df.mean()) |
|
1 2 3 4 5 |
身長(男子) 8014.2 体重(男子) 2955.6 身長(女子) 7406.0 体重(女子) 2497.0 dtype: float64 |
有効数字を変更したければ、先程と同じくお尻に「.round(有効数字)」を付けてください。
また、「平均値」でも、「男子の身長」だけで良いという場合は以下でOKです。
|
1 |
print(df.mean()["身長(男子)"]) |
|
1 |
170.51489361702127 |
こちらも「.round(有効数字)」が使えます。
それでは、平均値以外の関数も色々用意されてしまいますので、整理しておきます。
データの代表値を求める関数一覧
上記の例における「mean()」の部分を以下に変えるだけでOKです。
describeに存在するもの
| データ数 | count() |
|---|---|
| 平均値 | mean() |
| 標準偏差 | std() |
| 最小値 | min() |
| 第1四分位(25%点) | quantile(0.25) |
| 中央値(50%点) | median() |
| 第3四分位(75%点) | quantile(0.75) |
| 最大値 | max() |
第1四分位、第3四分位の書き方を見れば分かるかもしれませんが、カッコの中の数字を変えれば「小さい方から〜%の点」の値はどこでも計算できます。
describeに存在しないもの
describeメソッドでは計算されない代表値は以下のように求めます。
| 合計値 | sum() |
|---|---|
| 分散値 | var() |
| 最頻値 | mode() |
| 歪度 | skew() |
| 尖度 | kurt() |
| 最大値を取る項目名 | idxmax() |
| 最小値を取る項目名 | idxmin() |
歪度と尖度は使う場面は限られるかもしれませんが、データの代表値としては代表的なものなので掲載しました。
あと「idxmax」「idxmin」は便利です。例えば、「idxmin」を先程のデータに適用してみると・・・
|
1 2 3 4 5 |
身長(男子) 沖縄 体重(男子) 静岡 身長(女子) 沖縄 体重(女子) 沖縄 dtype: object |
なるほど。。。なんとなく考えさせられる結果です。
まとめ
これだけ押さえておけば、ざっくりとしたデータの集計はいつでも出来ます。
無論、上記の関数をすべて記憶しておく必要はなく、このページなどを参照しながらプログラムを書けばOKです。
もっと詳しく知りたい方は、以下の書籍などもおすすめです。
以上が、Pythonでデータ分析を始める際の第一歩となります。