非階層型クラスタリングの代表的手法である「k-means法」をPythonで実行してみます。
k-means法の理論についてはこちらの記事をご覧ください。

ファイルの読み込み、k-means法の実行
今回は理論編で使用したデータとほぼ同様の、以下のデータを用います。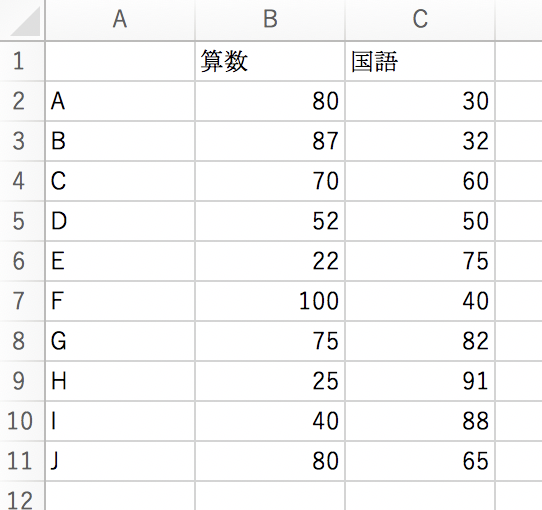
下記のようにファイルを読み込み、sklearn.clustar内のKMeansメソッドを用いれば非常に簡単に実行することができます。
|
1 2 3 4 5 6 7 8 |
import pandas as pd df = pd.read_csv("test_score.csv",index_col=0) from sklearn.cluster import KMeans vec = KMeans(n_clusters=3) vec.fit(df) print(vec.labels_) |
KMeansメソッドの引数「n_clusters」はクラス数です。
クラス数は人間が決めなければいけません。
今回は理論編との結果比較のため、3にしています。
結果は。。。
|
1 |
[1 1 2 2 0 1 2 0 0 2] |
もう出てきましたね。
「vec.fit(データ)」でK-meansが実行され、「vec.labels_」に予測クラスター番号が格納されます。
ちなみに「vec.fit_predict(データ)」とすると、一気にクラスの予測まで完了します。
結果には読み込んだデータの上から順番にクラスター番号が振られていますが、これでは何がどのクラスターになのか良く分かりません。
もう少し分かりやすくしてみましょう。
実行の度にクラスター番号は変わります。
また、それだけでなく、稀に結果も異なる場合があります。
K-means法は初期値をランダムに選ぶのでその影響ですが、デフォルトでは「K-means++」という、通常のK-means法よりパワーアップした手法で計算が行われており、実行の度に結果が変わる問題はそこまで起こりません。
クラスターごとの結果集計
まずは上記のクラスタリング結果をデータフレームに格納します。
データ分析を行う時は、どんな時でもデータフレームに値を突っ込んでから処理するのが結果的に楽かなという気がします。
今回の場合は非常に簡単で、
|
1 |
df["class"]=vec.fit_predict(df) |
とするだけです。すると、読み込んだデータフレームに行が追加され、
|
1 2 3 4 5 6 7 8 9 10 11 |
算数 国語 class A 80 30 1 B 87 32 1 C 70 60 2 D 52 50 2 E 22 75 0 F 100 40 1 G 75 82 2 H 25 91 0 I 40 88 0 J 80 65 2 |
このようになります。こうなればクラスタごとの傾向などがすぐに計算できます。
例えば、クラスタごとの科目別平均点を出したければ、groupbyメソッドを使って
|
1 |
print(df.groupby("class").mean()) |
とすれば、
|
1 2 3 4 5 |
算数 国語 class 0 29.00 84.666667 1 89.00 34.000000 2 69.25 64.250000 |
と集計できます。
結果を見ると、「クラス0」は国語が得意なグループ、「クラス1」は算数が得意なグループ、「クラス2」はバランスが良いグループ、と考えられます。
結果のグラフ化
グラフ化もしてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
#グラフ化 import matplotlib.pyplot as plt #グラフのデザイン指定 plt.figure(figsize=(6, 6)) plt.rcParams["font.size"] = 15 plt.xlim(0,100) plt.ylim(0,100) #プロット X = df["算数"] Y = df["国語"] plt.scatter(X,Y,color=colors) #点に色を付与 color_codes = {0:"red", 1:"blue", 2:"green"} colors = [color_codes[x] for x in vec.labels_] #点に名称を付与 for i,(x_name,y_name) in enumerate(zip(X,Y)): plt.annotate(df.index[i],(x_name,y_name)) plt.show() |
デザインはお好みで。
結果は・・・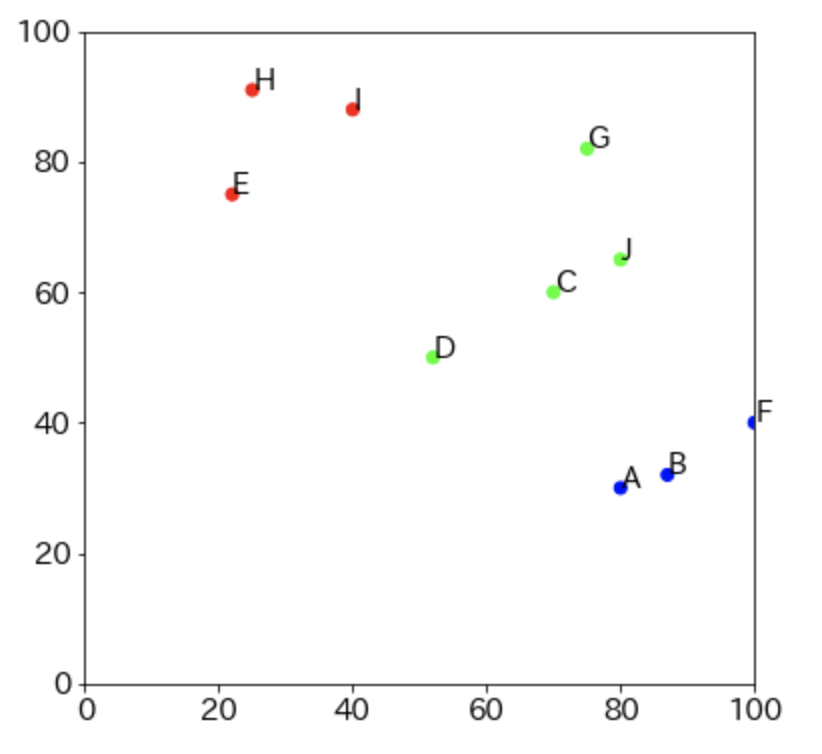
きちんとクラスタ分けされているみたいです。
ちなみに、「社会」「理科」など項目数が3以上ある場合は、まず次元削減を使って、項目数を2に落としてからグラフ化してください。
まとめ
K-means法は非階層型クラスタリングの代表格的手法です。
Excelで実行するのは難しいですが、Pythonでは非常に簡単に実行できます。
データをグループ分けしたい時には使ってみて下さい。
また、階層型クラスタリングでは実行方法が異なりますので、別の記事にしています。