AIの開発は通常のシステム開発に比べ、より数学の理解が必要になります。
・・・とは言われるものの、一体どこに何の数学の知識が必要なのでしょうか。
AI開発プロジェクトにおいては、開発者が知っておくべき数学の知識と、マネージャも知っておくべき数学の知識がそれぞれ存在します。
JDLA主催のディープラーニングG検定・E資格に出題される数学の分野も、おおよそこの範囲となります。
AI開発に数学が必要な部分
まず、AI開発で数学の知見が必要となってくる部分は大きく2つに分けられます。
1つ目は「AIの理論を理解するための数学」です。
ディープラーニングを始めとした機械学習はすべて数学の理論に基づき動作しています。
便利な時代ですので、数学のことを知らなくても、ネット上に落ちているソースなどを参考にすれば機械学習の実装は出来てしまいます。
しかし、AIの実装の後には、その精度向上のためのパラメータチューニングが必要です。
闇雲にハイパーパラメータをいじれば性能は少しは上がるかもしれませんが、機械学習の計算理論を知っていなければ適切なチューニングを行うことができません。
このあたりの理解が、「なんちゃってAIエンジニア」と「AIエンジニア」の垣根となってくるかなと思います。
2つ目は「性能を評価するための数学」です。
こちらは開発者だけでなく、マネージャでも正しく理解しておかないといけません。
AIの性能というのは必要不可欠な要件定義のひとつです。
その性能をどう測るのか、そしてどれだけの性能が必要なのか・・・きちんと顧客とすり合わせて置かなければ、後に問題になりかねません。
性能評価の指標も色々と存在しており、適切な指標はシステムにより異なります。
このあたりの知識と勘所は、開発者のみならずマネージャの立場でも必要となります。
では、それぞれについて特に必要な数学の分野について見ていきます。
理論を理解するための数学
もちろん不必要な分野などは無いのですが、特に大切な数学の分野が3つあります。
それは「微分」「線形代数」「確率・統計」の3つです。
順番を追って説明します。
微分
機械学習の計算方法は多くの場合、
適当なパラメータで実行⇒性能を評価⇒その結果を見てパラメータ調整⇒再実行…
という流れを何回も繰り返し、性能を上げていくという手順を踏みます。
この、「結果を見てパラメータ調整」という部分・・・ここに微分の力が発揮されます。
たとえば、パラメータが1つだけの簡単な機械学習モデルを考えてみます。
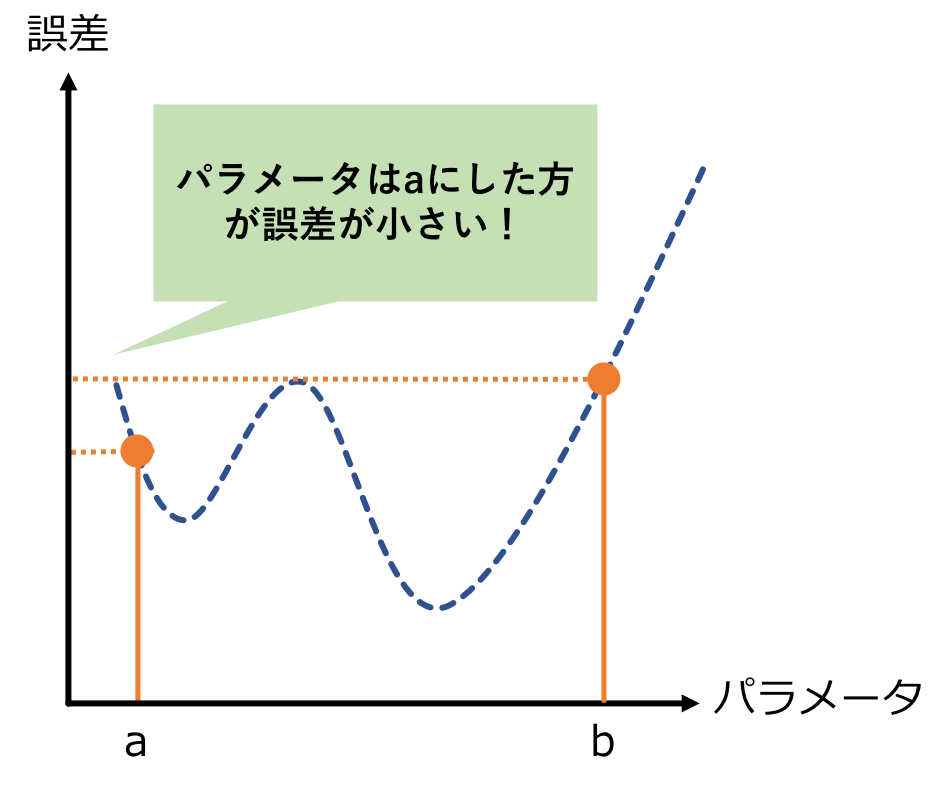
横軸がパラメータ、縦軸が誤差の大きさ(小さいほどAIの性能が良い)となっています。
便宜上、適当な関数を描いていますが、この関数がどんな形なのかは誰にも分かりません。
ですが、適当なパラメータを入れて計算すると、その点における誤差の大きさが分かります。
パラメータの値を変えれば、その点における誤差の大きさが分かります。
・・・これを繰り返していけば、最も誤差が小さな点が徐々に浮き彫りになっていきます。
「機械学習の性能を上げる」という事は、この「誤差が最も小さい点を探る」行為と同じです。
しかし、ランダムにパラメータの値を入れていると時間が掛かります。
より効率的にパラメータを調整していきたいところです。
そこで、誤差の値を計算すると共に、この点で関数を微分した値も計算します。
その点で微分した値が+だった場合、関数の傾きが右上がりだと分かるので、もっとパラメータを左に調整した方が誤差が小さくなりそうと予想できます。
逆に-だった場合、もっとパラメータを右に調整した方が誤差が小さくなりそうと予測できます。
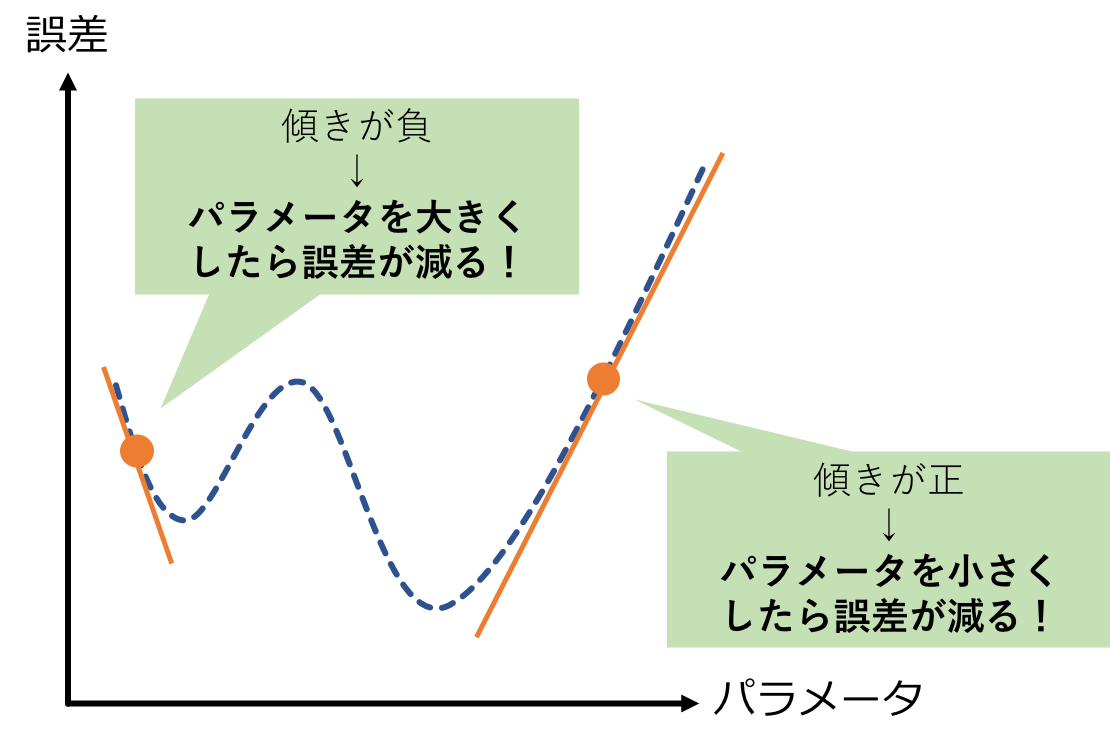
これが、機械学習における「微分」の重要性です。
この例では1パラメータでしたが、2つ以上になっても「偏微分」を使えば全てのパラメータの傾きを知ることが可能です。
線形代数
お次は線形代数です。
線形代数といっても、機械学習の理解に必要なのはベクトルと行列の演算方法が主です。
ベクトル・行列の素晴らしいところは何と言っても、たくさんの計算を1回で行えることです。
上で微分の重要性を述べましたが、機械学習のモデルが複雑になればなるほど何回も微分計算が必要になりますので、できれば簡素に計算を行いたいところです。
そんな時、行列を用いれば、すべてのパラメータの微分を一回の計算で行うことができます。
実際にプログラムを組む際にも、単純かつ分かりやすくなりますので、行列演算を使わずに機械学習のアルゴリズムを実装することはほぼありません。
基本的な行列の演算処理については理解しておくことが望ましいでしょう。
確率・統計
3つ目は確率・統計です。
これは開発者に限らず重要なところではありますが、機械学習の実装という面においては「モデルの性能がどれほど良いのか」を評価するために必要不可欠です。
同じ正解でも、それが自明な結果である場合もあれば、偶然に正解している事もあります。
同じ不正解でも、あまりに異常値すぎて放置してよい不正解なのか、頑張れば正解にできる不正解なのか。
しかし、それをデータごとに判断するのはほぼ不可能なため、確率・統計的にこのあたりを判断、調整していきます。
このことから、学習モデルを正しく評価するために確率・統計の知識が必要となります。
性能を評価するための数学
続いては、性能評価に用いる数学です。
要件定義段階で、性能の計算方法と、性能の許容ラインについては必ず顧客合意が必要ですし、納入前に最終的な性能結果を提示する事も必須です。
よって、ここに関しては開発者のみならず、マネージャであっても正しく理解しておく必要があります。
混同行列
AIのタスクが「分類問題」であった場合、その精度を計算するために必ずと言って良いほど作成するのがこの「混同行列」です。
どれほど分類が正解しているのかを見る表ですが、ただのクロス集計だと侮ってはいけません。
詳細は下記の混同行列の記事に譲りますが、この集計表から「精度」に落とし込むには様々な方法があり、どの指標が優れるのかは時と場合によって変わります。
混同行列を正しく理解し、適切な指標を選ぶ勘所を持つことが大切になります。

誤差指標
AIのタスクが「回帰問題」(数値を予測する問題)であった場合、その精度を計算するのに「誤差指標」を用います。
数値予測の場合は混同行列が作成できませんので、結果と予測の数値誤差を見ていくことになります。
この誤差の測り方の指標にもたくさんあり、分類問題と同様に、どの指標が優れるのかは時と場合によって変わります。
ここも適当に選ばず、適材適所な誤差の指標を選ぶように心がけましょう。
まとめ
以上を整理すると、AI開発プロジェクトに従事するに当たって必要な数学的な知識・思考は、
開発者・・・「微分」「線形代数」「確率・統計」の概念を理解し、簡単な計算が出来ること
開発者+マネージャー・・・「混同行列」「誤差指標」といった性能評価指標を理解し、タスクに応じて適切な指標を選択できること
・・・このあたりに集約されます。
無論、マネージャーであっても微分などの知識はあった方が良いですし、ここに出てきていない数学の知識を持っていればなお良いでしょう。
しかし、AI開発に携わるのであれば、上の分野を重点的に学んでおくことが良い開発者になるための近道になるかと思います。