非階層型クラスタリング「k-means法」の計算過程

クラスタリング手法の中でおそらく最も広く使用されている手法、k-means法(k-平均法)について説明します。

クラスタリングの概要については以下に整理しています。

「クラスタリング」とは何に使える？どんな手法がある？

k-means法のアルゴリズム

k-means法は以下の手順でデータをグルーピングしていきます。
今回は説明の都合上、「算数」「国語」の2次元(x軸とy軸)でご説明します。
ちなみに、「算数」「国語」だけでなく「英語」という科目が加われば3次元で考える事になりますし、
さらに「理科」「社会」が加われば5次元でこの処理を行うことになります。
ただ、それを図示するのは辛いので、今回は「算数」「国語」だけでご説明します。

①.グループ数を決定する

まずは、人間が何グループに分割するかを決定します。
今回はグループ数=3としてみます。

②. 適当にグループを割り当てる

まずは、何も考えずにすべての点を3グループのいずれかに振り分けます。

③. グループごとの重心を求める

グループごとに、その重心を計算します。（図中の✕記号）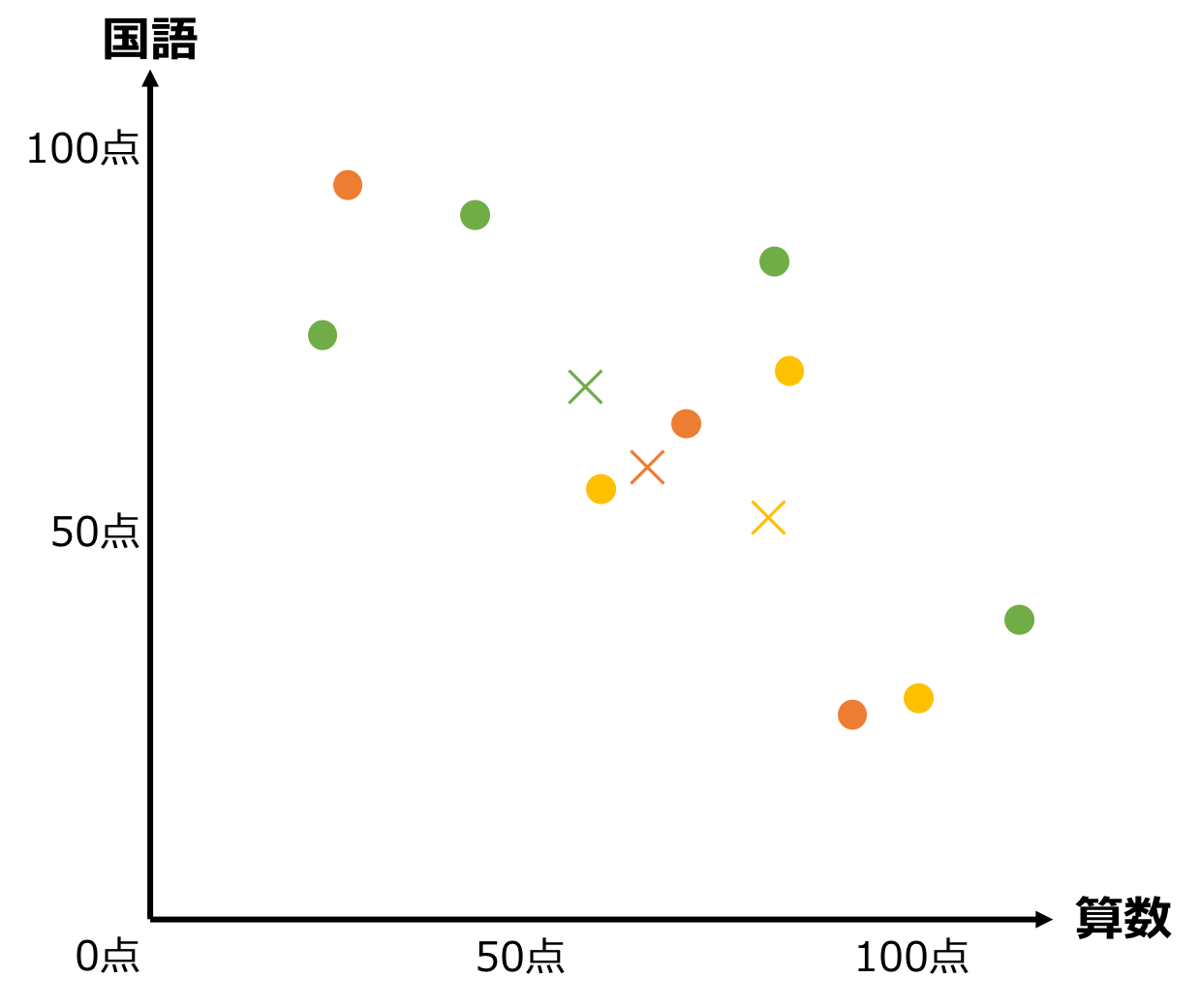

④. すべての点を、最も近い重心のグループに配置し直す

すべての点について、最も近い✕記号のグループに再配置します。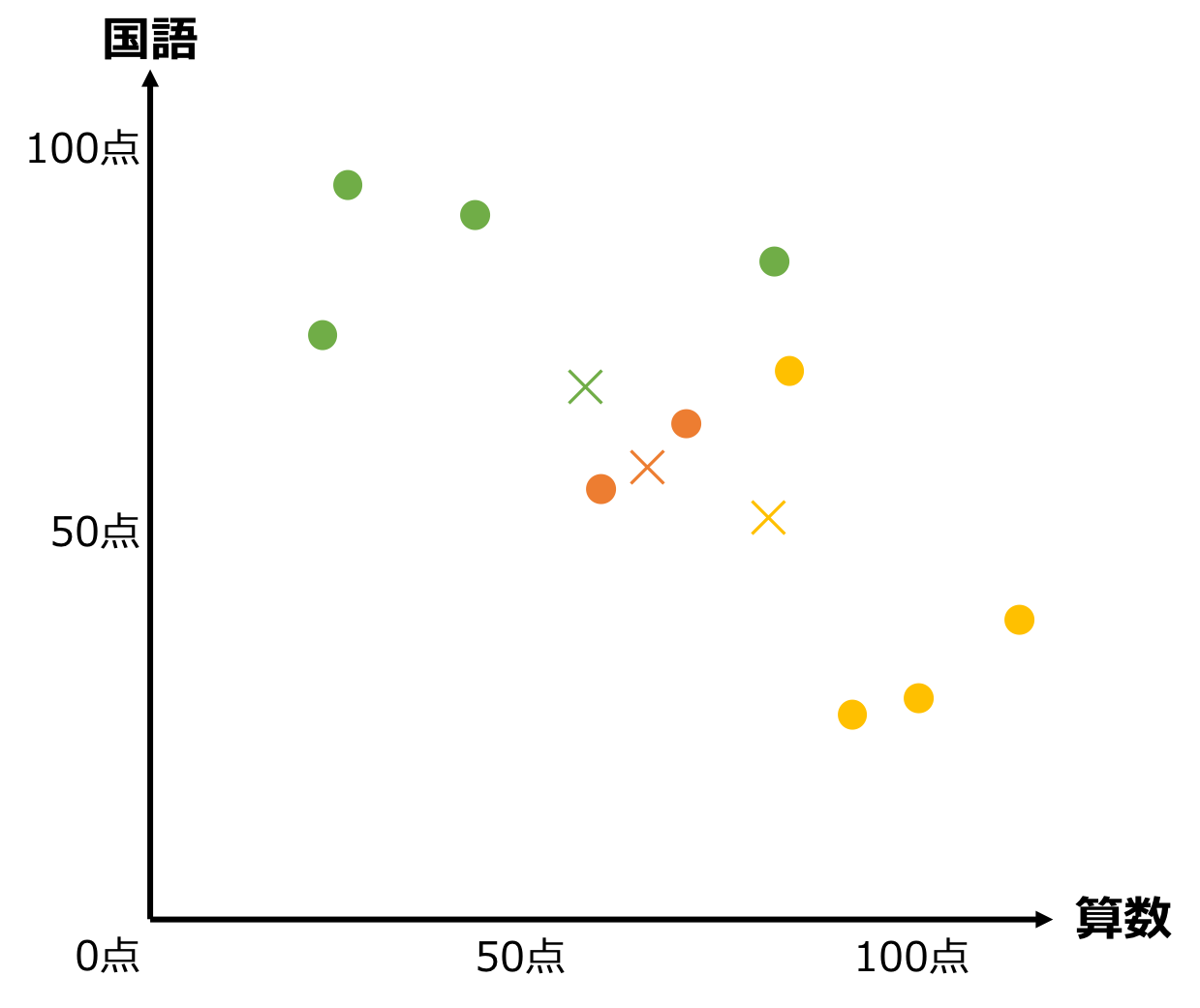

⑤. 新グループで再度、重心を求める

グループが変わったので、それぞれの重心も変わります。再度、重心を計算します。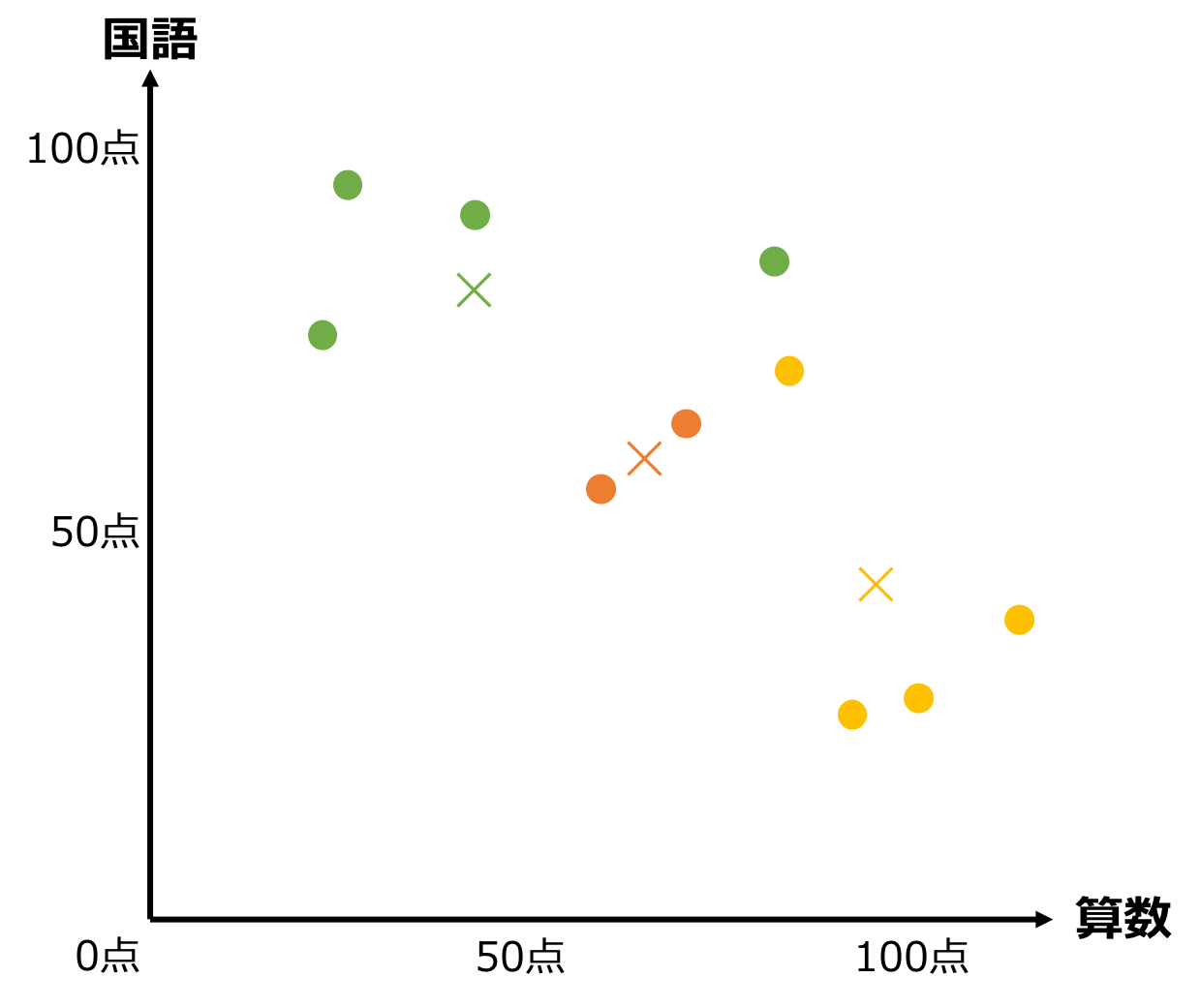

⑥. すべての点を、最も近い重心のグループに配置し直す

改めてすべての点について、最も近い✕記号のグループに再配置します。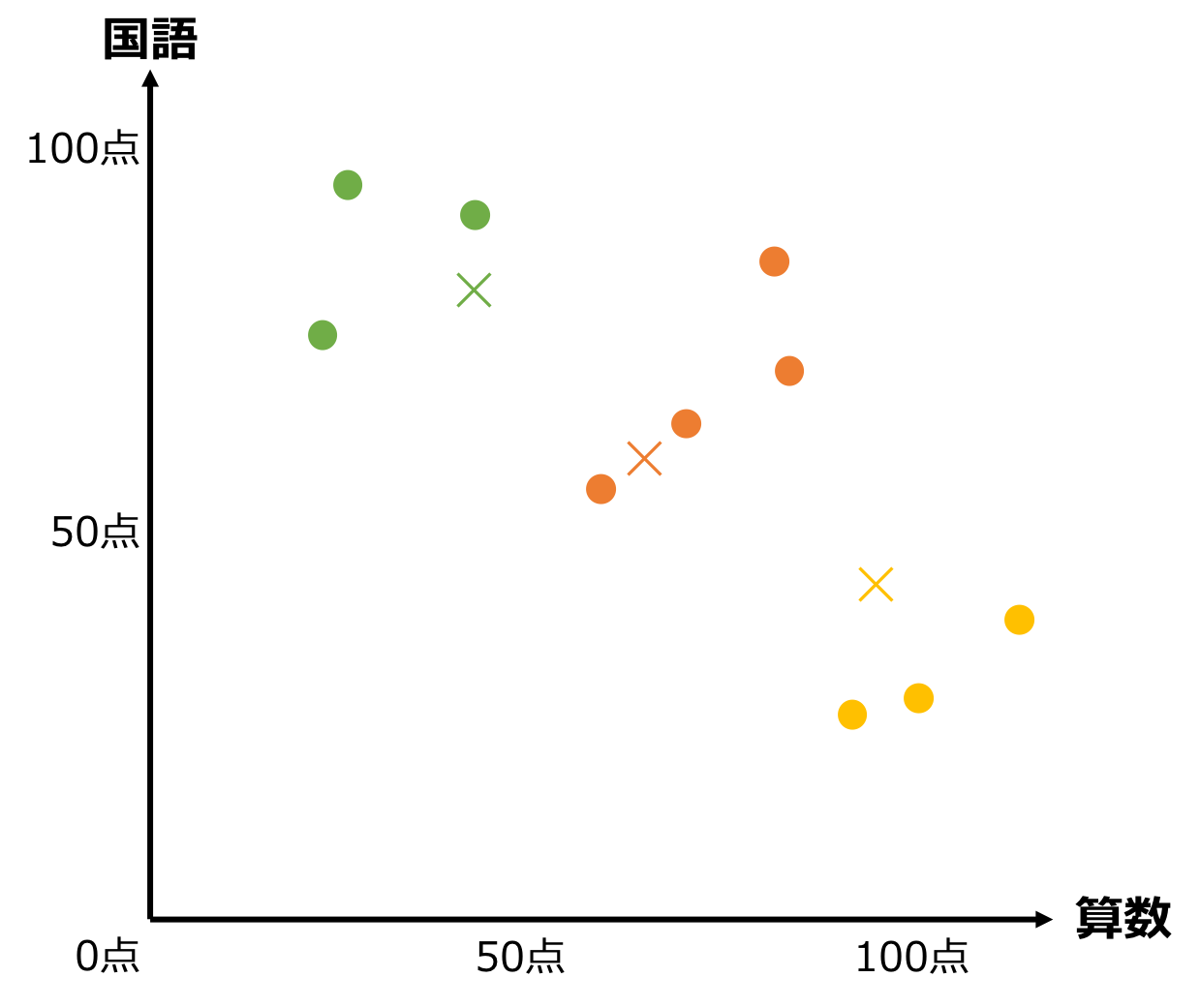

⑦. ⑤〜⑥をグループが変動しなくなるまで繰り返す

以上の作業を、グループが変わらなくなるまで何度も何度も繰り返します。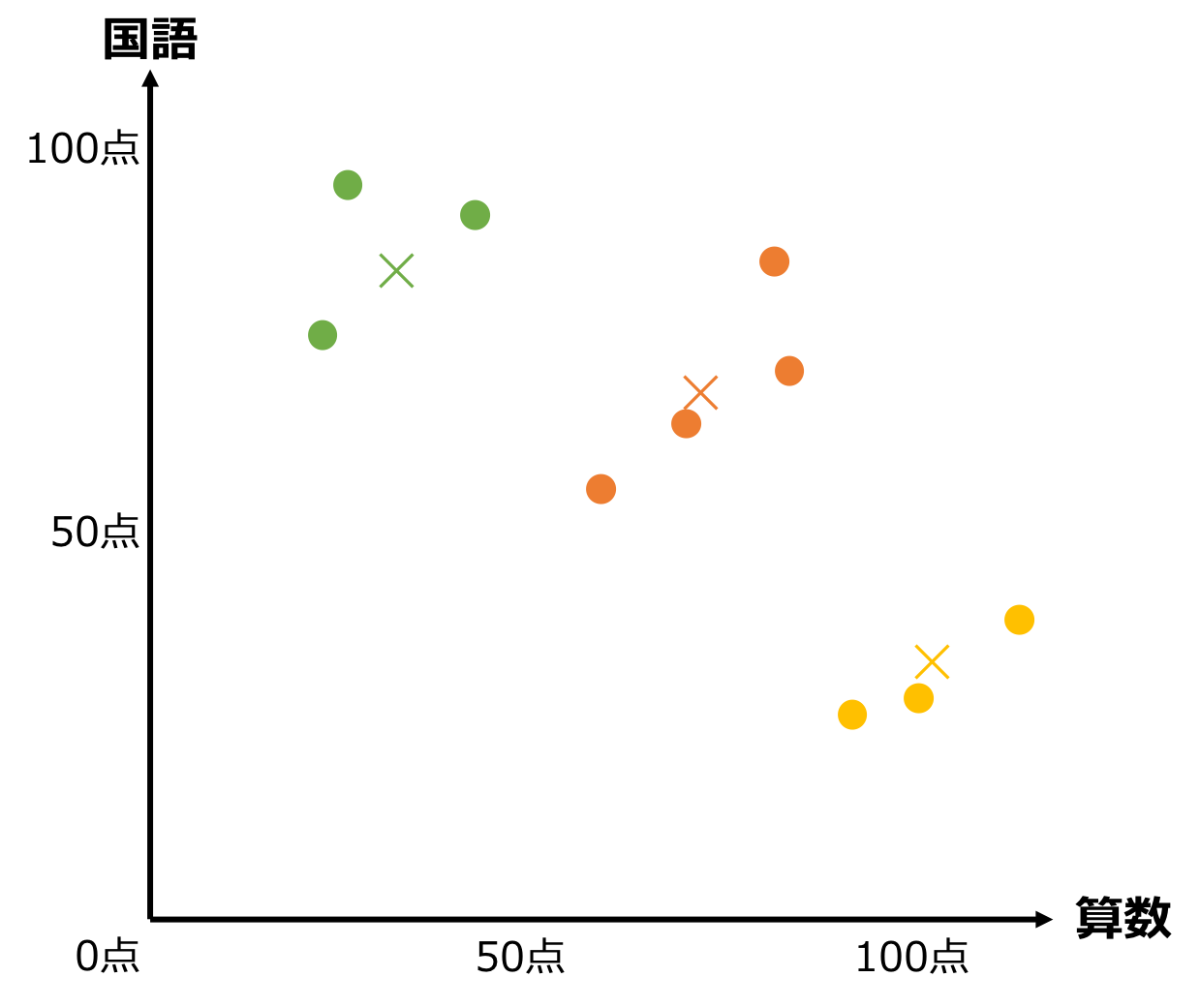

⑧. グループが変動しなくなったらグループ分け完了！

グループが変わらなくなったら、処理完了です。無事に、すべての点を3グループに分類できました。

k-means法の問題点と改良アルゴリズム

収束するまでにどれだけ時間が掛かるのか分からない

「グループが変動しなくなったらグループ分け完了」とは言っても、一体何回⑤〜⑥の処理を繰り返せば処理が完了するのか分かりません。
そのため、k-means法では「指定回数だけ繰り返しても収束しなかったら、そこで強制的に処理終了する」という事を始めに決めなければいけません。
この指定回数を幾つにすれば良いのかは時と場合によって異なるので一概には言えませんが、Pythonのscikit-learnパッケージには初期値に300が指定されているので、私はとりあえず300回にして、結果が悪ければ1000回にしてみる、というように考えています。

ランダム割り当ての仕方により結果が異なる場合がある

グループ数を決めた後、上記②は完全ランダムに振り分けられます。
これにより、収束までの時間が変わってしまうだけでなく、得られる結果まで異なるという事もよくあります。
その問題を解決したアルゴリズムのひとつにK-means++法があり、初めからこちらを用いる場合も多いです。

適切なグループ数は人間が決めなければいけない

初めから幾つのグループに分割したい、と決まっている場合は良いのですが、適切なグループ数が幾つか分からない、という場合も往々にしてあります。
その場合は、適切なグループ数も含めて検討してくれるアルゴリズムを選択することになります。
代表的な手法にx-means法があり、これは、グループ数を2,3,4…と色々実験し、その中で最もグループ分けが上手く行った時のグループ数と、その結果を出してくれるものです。