様々あるデータ分析手法の中でも非常に活躍の機会が多い「クラスタリング」ですが、一体クラスタリングとは何なのでしょうか?
一概に「クラスタリング」と言っても、その手法は様々です。
それらの意味をきちんと理解して使わなければ、正しく分析を行えない上に、その価値を最大限に活かすことができません。
本記事ではクラスタリングの概要について整理しました。
クラスタリングとは
「クラスタリング」というのは、一言で言えばデータを自動でチーム分けする手法です。
例えば、あるクラスで国語と算数のテストを行って、その点数を元に「理系」「文系」に分ける・・・ようなイメージです。
例えば下図のような、あるクラスにおける算数と国語のテスト結果を座標にプロットしたとします。
そうすると、以下のように「算数が得意なグループ」「国語が得意なグループ」「バランスの良いグループ」になんとなく分けられるかと思います。
このように状況がシンプルであれば人間が目で見ても分かりますが、試験科目に「理科」「社会」「英語」「体育」「音楽」・・・などが追加されたり、グループに「体育会系」「芸術系」・・・などこちらまで増えたり、しかも学生数が1000人以上などなったら、とても人間が分類するのは大変です。
そこで、自動的にチーム分けする方法が必要になるわけです。
グループ分けすることにより、全学生の傾向をつかみ、グループごとに違う施策を打つ、などという処理が簡単に出来るようになります。
2種類のクラスタリング手法
ここからは具体的なクラスタリングの手法についてです。
クラスタリングの手法は大別すると、「階層型クラスタリング」と「非階層型クラスタリング」の2つに分かれます。
「階層型クラスタリング」とは、沢山のデータの中から近いもの同士をくっつけて行って、最終的に「デンドログラム」を作成します。
デンドログラムとは、「全てのデータの関係性」を表現したトーナメント表のような図です。
それに対して「非階層型クラスタリング」は、全てのデータの関係性をひとつにまとめる事はせず、単純にデータをチーム分けするだけの手法です。
以下のようなイメージです。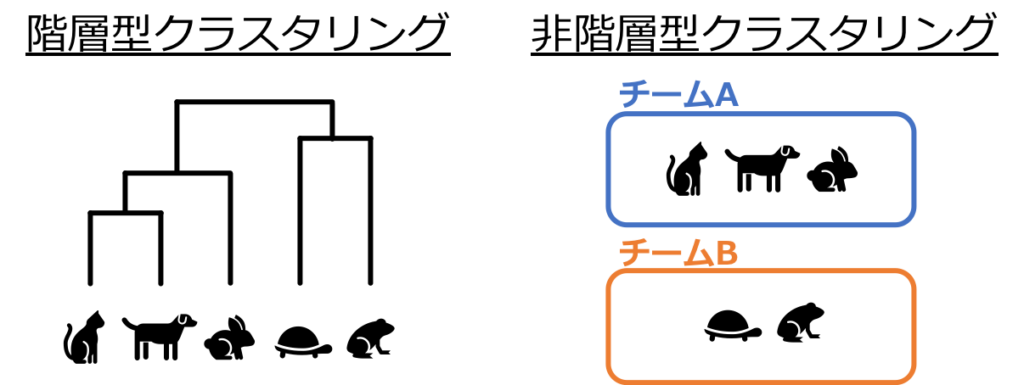
以下、それぞれについて整理します。
階層型クラスタリング
階層型クラスタリングは、「ウォード法」「群平均法」「最長距離法」「最短距離法」・・・などと様々な手法があります。
最終的にデンドログラムを作成することは一緒ですが、その計算過程がすべて異なります。
色々あるのですが、絶対的にどれが優れる、と言えるような花形の手法は無いように感じます。
しいて言えば、特にこだわりの無い場合は「ウォード法」がやや使用頻度が高いかと思います。
具体的にどのように計算を行っているかは、以下の記事に整理しました。

Pythonでの実行方法については以下に整理しています。

非階層型クラスタリング
種類の多い階層型に対して、非階層型クラスタリングは、ほぼ「K-means法」(もしくはそれを派生させた方法)の一択です。
ただし、K-means法では計算に乱数が用いられている関係で、実行のたびに結果が変わります。
もちろん、結果が変わらないように指定することも可能ですが、デフォルトでは結果が変わる場合があることにご留意ください。
どのように計算を行っているかは、以下の記事に整理しました。

Pythonでの実行方法については以下に整理しています。

最後に
以上、クラスタリングについてでした。
一言で「クラスタリング」といっても様々なやり方がありますので、タスクに応じて適切な手法を選択するようにしましょう。