階層型クラスタリング(ウォード法、群平均法など)の計算過程

クラスタリング手法の一つ、階層型クラスタリングの計算過程について整理しました。
階層型クラスタリングと一言で言っても様々な方法があるのですが、本記事では代表的な4手法について説明します。

クラスタリングの概要については以下に説明しています。

「クラスタリング」とは何に使える？どんな手法がある？

データの準備

さて、今回は一例として、以下の「5名の数学と国語のテストの点数」データをクラスタリングしてみます。

 

名前	数学	国語
Aさん	70点	90点
Bさん	100点	80点
Cさん	50点	90点
Dさん	80点	60点
Eさん	40点	100点

手順1：全ての要素同士の「距離」を求める

何はともあれ、まずは全ての要素同士の距離を計算します。
つまり「AさんとBさんの近さ」「AさんとCさんの近さ」・・・を数値化していきます。

この「距離」にも色々な種類があるのですが、今回は最もポピュラーな「ユーグリッド距離」を用います。
「ユーグリッド距離」とは、単純に定規で計測した2点間の長さの事です。

さて、上記の5人の点数データを図にして、ユーグリッド距離で任意の2人の距離を数値化してみましょう。

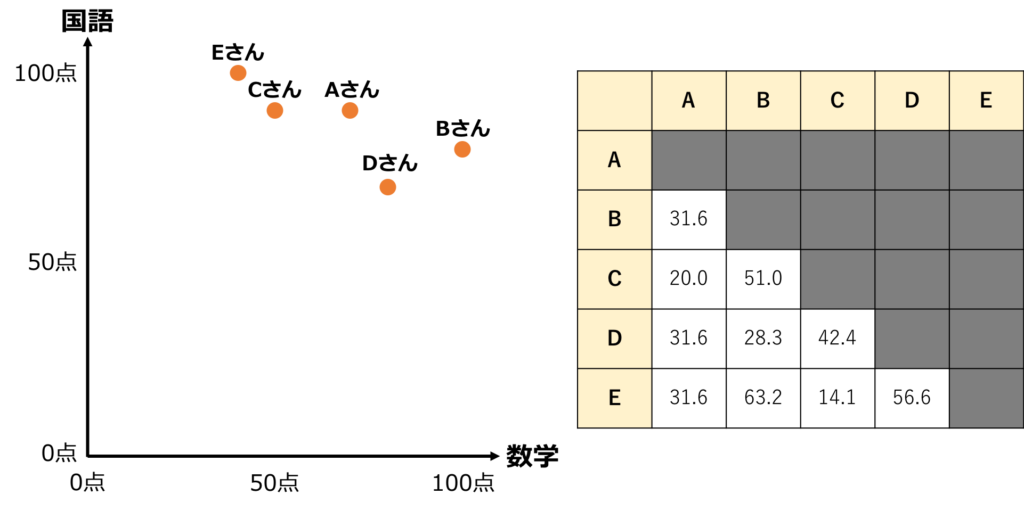
これで、クラスタリングするための準備は完了です。
次から、いよいよデンドログラム（トーナメント表のような図）を作っていきます。

手順2：ペアを作る

全てのペアについて距離が計算できたので、お次はグルーピングしていきます。
第一歩目は簡単で、一番距離が小さいものをくっつけます。この例で言うとCとEが14.1で一番小さいですので、まずはCとEをくっつけます。
ここからはもうCとEは一つのカタマリで離れることはありません。

CとEが一心同体になったので、データの数が5から4に減りました。
ということは、先程の「行列」も5×5から4×4にしなければなりません。
やってみましょう。

先程まではなかった、「AとCE」「BとCE」「DとCE」の距離が分からないので、埋められませんね。
さて、この新しく定義しないといけない距離・・・この計算方法が「最小距離法」「最大距離法」「群平均法」「ウォード法」で異なるのです。
逆に言えば、手法の違いはここだけです。
では、次の章でそれぞれの「新しい距離」の計算方法を見ていきます。

手順3：距離の情報を更新する(手法別)

それでは、手法ごとの違いを見ていきます。

最短距離法(Minimum Distance Method)

最短距離法とは、くっつけた2つのうち、短い距離を用いて距離を更新する方法です。
先程の例で言えば、「AとC」「AのE」の距離のうち、短いほうの距離を「AとCE」とするわけです。
「AとC」は20.0、「AとE」は31.6ということは、「AとCE」の距離は20.0となります。
同様に先程の表を全部埋めると、以下のようになります。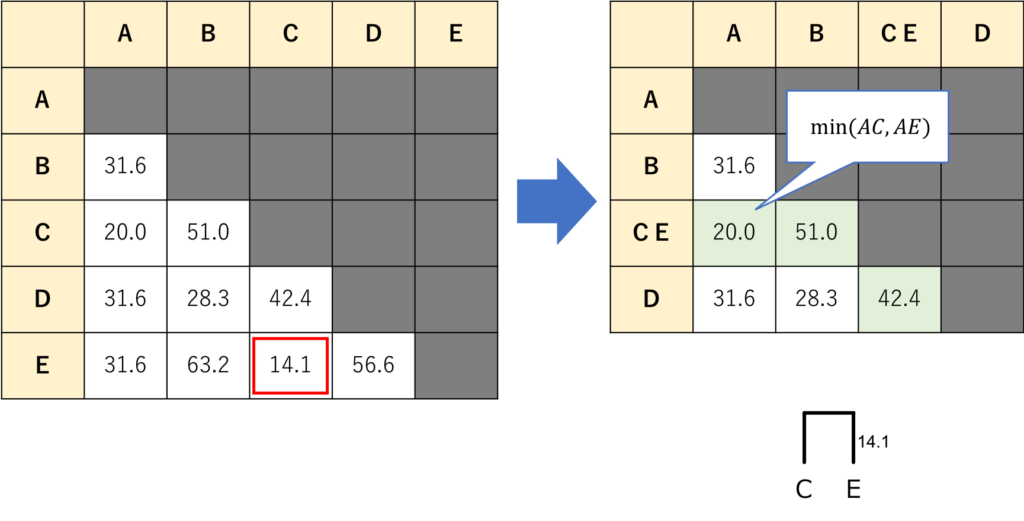

これで、4×4の行列が出来ました。
あとは、同様に「行列の中でもっとも小さい数字」をくっつける、という処理を繰り返していくだけです。
最後までやってみましょう。

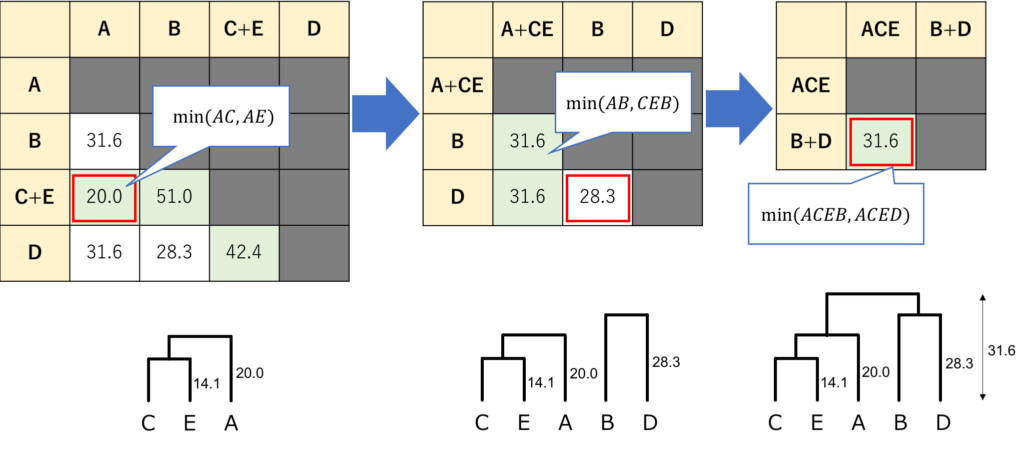
無事に、全部のデータがくっつきました。
これで最短行列法によるクラスタリングは完成となります。

最長距離法(Maximum Distance Method)

最長距離法とは、くっつけた2つのうち、長い距離を用いて距離を更新する方法です。
最短距離法の逆ですね。
先程の例で言えば、「AとC」「AのE」の距離のうち、長いほうの距離を「AとCE」とするわけです。
よって「AとCE」の距離は31.6となります。

この「距離の更新」の計算が違うだけで、あとは同じです。
全てくっつくまでやってみましょう。

これで最長距離法によるクラスタリングは完成となります。

群平均法(Group Average Method)

群距離法とは、2つのデータをくっつける時に、そのすべての距離の平均を新たな距離とする方法です。
別名「平均距離法」や「非加重結合法(UPGMA)」とも呼ばれます。

先程の例で言えば、「AとC」「AのE」の距離の平均を「AとCE」とするわけです。
よって「AとCE」の距離は25.8となります。

ちなみに、3×3の行列において、「ACE」と「B」の距離は「AB」「CB」「EB」の3つの平均値になります。
最初の行列から3つ数値を引っ張ってきて計算しても良いのですが、式変形を行うと1つ前の行列の情報から以下の公式で更新された距離の更新を行えるようになります。

これを踏まえてクラスタリングを最後まで行ってみると、以下のようになります。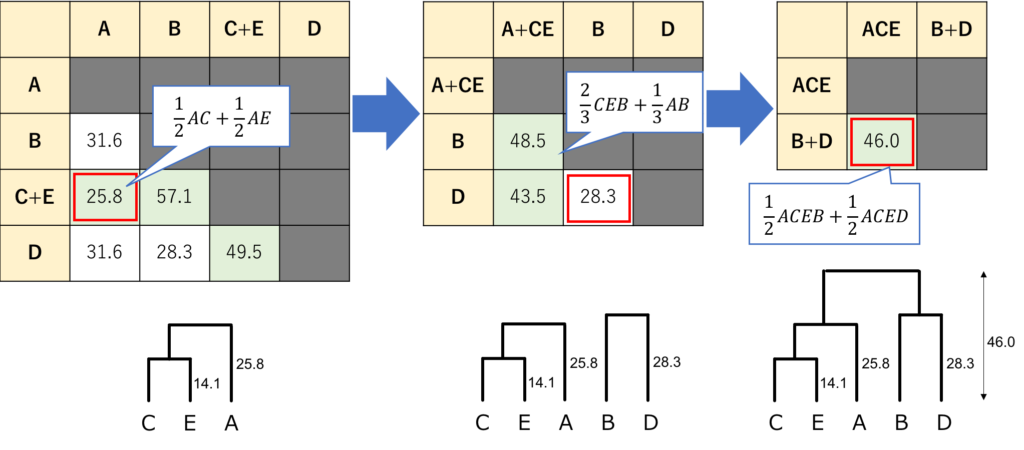

これで群平均法によるクラスタリングは完成となります。

ウォード法(Ward’s Method)

ウォード法とは、「チームのばらつき具合(分散)」が最小になるようにデータを結合していく方法です。

先程の例で言えば、「ACEのばらつき」から「Aのばらつき」「CEのばらつき」を引いた値を「AとCE」とするわけです。
「結合した後のばらつき」の大きさから、「もうくっ付いてしまっているのでどうしようもないばらつき」の大きさを引く感じです。

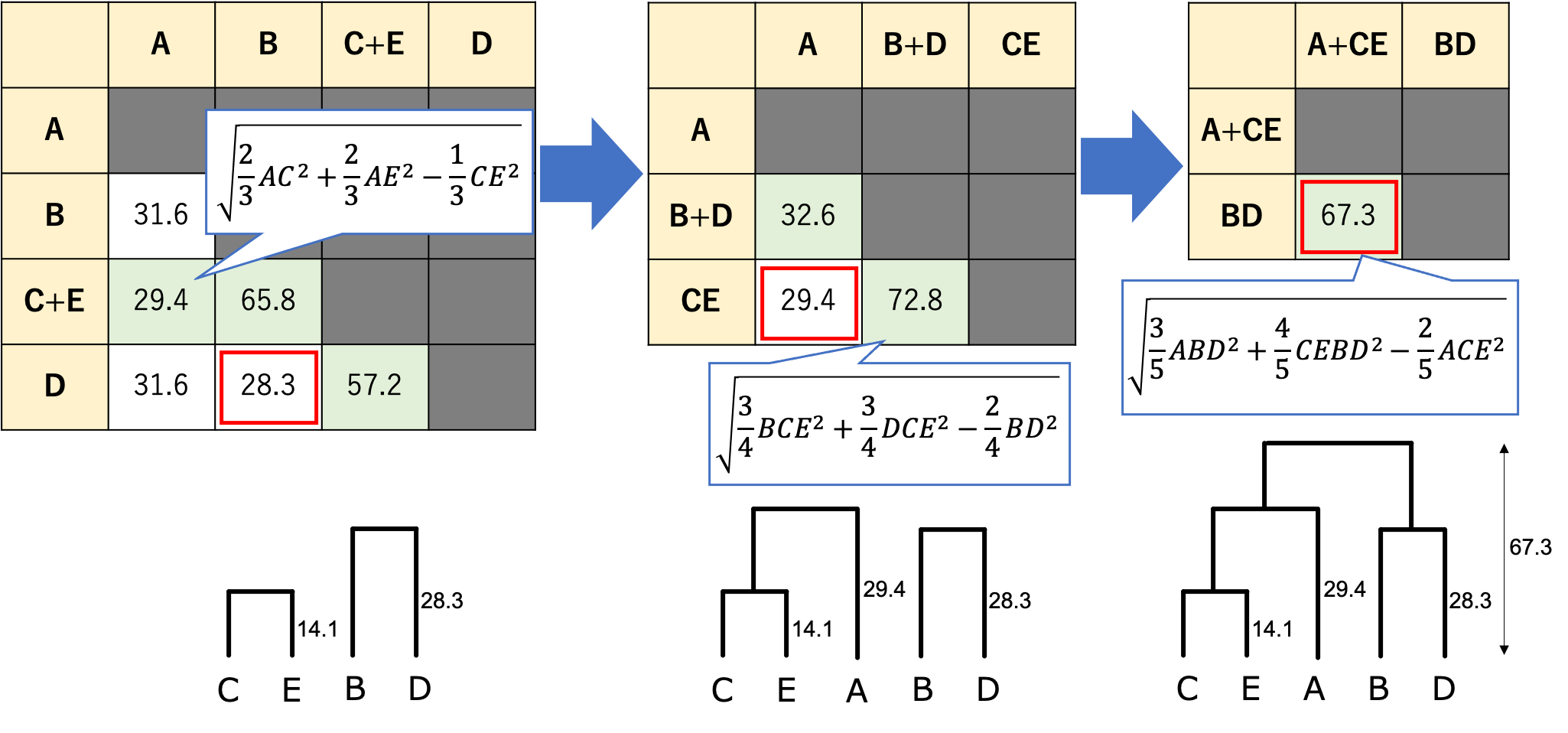
分散の計算が入るので少々計算が面倒ですが、以下の式に従うと1つ前の行列の状態から「距離の更新」を行うことができます。

この式に当てはめると、「AとCE」の距離は29.4となります。

どの手法を選べばよいのか？

さて、4方法を見ていきましたが、手順はどれも一緒で、単に「2つくっつけた後の距離の更新方法」が違うだけでした。
しかしそれによりクラスタリング結果も違う結果となりました。

一体、どんな時にどの手法を選べばよいのでしょうか。
個人的な意見も入りますが、特にこだわりが無ければとりあえずウォード法を選択しておき、もし何か理由があるならばそれ以外の手法を選ぶという方針で良いかと思います。
単純に使われている事例が多いからというのと、計算は面倒でも「分散を最小にする」という方針自体が非常に分かりやすいと感じるからです。

この4手法の中では最も計算がややこしく、処理時間はかかりますがそれは微々たるものです。
あとは「もっとも短い距離でクラスタリングしたい」という明確な理由があるならば最短距離法にしよう！と判断する場合もあるでしょうが、あんまりそんなタイミングは無いかなあと。

・・・ということで、「階層型クラスタリング」をしたくて、その手法に困るのならばウォード法にしておきましょう。
その結果に不満があったりしたら他の手法で描いてみてもいいかもしれません。
とはいえ、自分にとって都合の良い結果を選択すれば良いわけではなく、その妥当さ、結果や方法論の説明しやすさ、といった観点で選ぶようにしましょう。