よく考えないと騙されてしまいそうな、確率・統計のトリックの中でも有名なもののひとつです。
まずは、以下の文章をご覧ください。
その医者に診察を受けると、「あなたは病気なので、今すぐこの薬を購入しなさい」との診断を受けた。
薬を買うべきか?
普通に考えれば、99%で当たるのならばほぼ正しい(=自分は病気である)と判断し、迷わず薬を購入すべきと考えられます。
…しかし、結論から述べるとそう考えるのは早計です。なぜでしょうか?
「99%」の分母と分子を見てみよう
ここで、「99%」という確率が、いったいどういった計算で算出されているのか・・・という面に目を向けてみましょう。
まず実際問題として、病気にかかっている人というのは少ないはずです。圧倒的に病気でない人のほうが多い。
では、仮に、実際に病気にかかっている人は100人。かかっていない人は10万人としてみます。
診察を受けた人は、これらを合計した10万100人です。
その中で、「99%の確率で当たる」と言うことは、
実際に病気にかかっている100人のうち、「病気」と申告されるのは99人、「病気でない」と申告されるのは1人、という計算になります。
一方で、実際に病気にかかっていない10万人のうち、「病気」と申告されるのは1000人、「病気でない」と申告されるのは99000人になります。
つまり、10万100人のうち、「病気」と申告されるのは99+1000=1099人いるわけです。
しかし、本当に病気なのはそのうち99人。
ということは、「病気」と申告された1099人のうち、本当に病気を持っているのは1割以下の99人だけです。
99%の確率で病気を当てる医者に「病気」と告げられたのに、実際に病気である確率は10%以下。何だか変な感じです。
混同行列を書いてみる
さて、どうしてこのような錯覚が起こるのでしょうか。
ここで「混同行列」の出番です。混同行列については以下をご参照ください。

混同行列を使うと、この事例は以下のようにまとめられます。
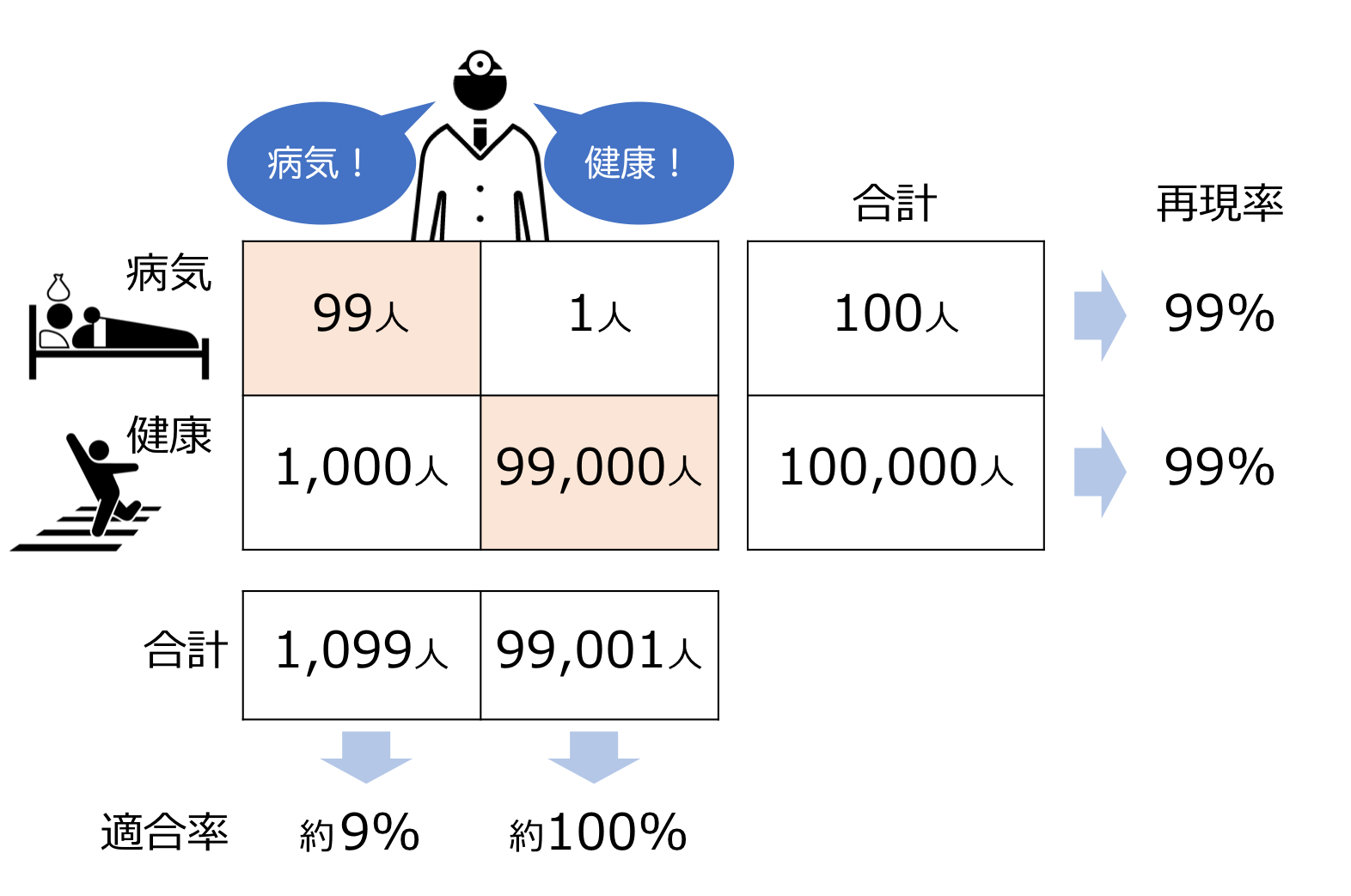
そう、「99%で当たる」と言うのはあくまでも「再現率が99%」という意味なのです。
「自分は必ず病気である」という前提において検査を受けたら、99%それは当たっていると。
逆に、「自分が病気だと言われた」という前提であれば、それが正解である確率は約9%です。これが「適合率」にあたります。
この「前提条件」の違いがあるために、「世間的に言われる確率(再現率)」と「体感的な確率(適合率)」にズレが生じてしまうわけです。
「99%の確率で当たる」という触れ込みに全くウソはありません。ただしこれは再現率であることを十分に理解する必要があります。
前提が分かって検査を受けに行く人は居ませんので、我々が気にしなければいけないのは適合率です。
その確率がどう計算されたのかをよく考えて、正しい決断を下せるようにしましょう。